「scikit-learnでPCA散布図を描いてみる」では、scikit-learnを使ってPCA散布図を描いた。 ここでは、scikit-learnを使って非線形次元削減手法のひとつt-SNEで次元削減を行い、散布図を描いてみる。
環境
「scikit-learnでPCA散布図を描いてみる」を参照。
MNISTデータセットとPCA散布図
MNISTデータセットは0から9の手書き数字を表す8x8グレイスケール画像のデータセットであり、irisに並んで有名なサンプルデータセットである。
このデータセットについてPCA散布図を描いてみると次のようになる。
%matplotlib inline import matplotlib.pyplot as plt from sklearn import datasets from sklearn.decomposition import PCA digits = datasets.load_digits() print digits.data.shape # (1797, 64) print digits.target.shape # (1797,) X_reduced = PCA(n_components=2).fit_transform(digits.data) print X_reduced.shape # (1797, 2) plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=digits.target) plt.colorbar() # <matplotlib.colorbar.Colorbar at 0x7f880818e6d0>
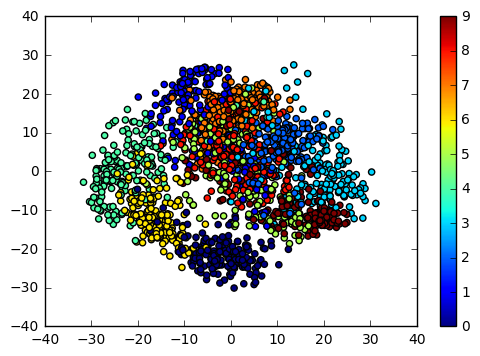
PCA散布図はデータのばらつきをプロットするにはよいが、次元削減により主成分ベクトルが作る線形空間での近似となるため、PCAが仮定している多次元正規分布から大きく離れた分布に従うデータでは高次元の特徴量が持っていた情報の多くが失われてしまう。 このようなデータに対しては非線形次元削減あるいは多様体学習と呼ばれる手法を用いることで、高次元空間における距離をもとにした次元削減を行うことができる。 いくつかの手法の概要をまとめると次のようになる。
- Locally Linear Embedding (LLE): データポイント近傍での線形性を仮定する
- Spectral Embedding (Laplacian Eigenmaps): 距離の近いデータポイント同士を繋ぐことで得られるグラフ構造を用いる
- Multi-dimensional Scaling (MDS): データポイント間の距離の大小をできるだけ保つ
- t-Distributed Stochastic Neighbor Embedding (t-SNE): データポイント間の類似度を表現する条件付き確率をできるだけ保つ
ここでは、2、3次元への次元削減において高いパフォーマンスを示すt-SNEを用いる。
MNISTデータセットのt-SNE散布図を描いてみる
t-SNEで2次元に次元削減して散布図を描いてみると次のようになる。
%matplotlib inline import matplotlib.pyplot as plt from sklearn import datasets from sklearn.manifold import TSNE digits = datasets.load_digits() print digits.data.shape # (1797, 64) print digits.target.shape # (1797,) X_reduced = TSNE(n_components=2, random_state=0).fit_transform(digits.data) print X_reduced.shape # (1797, 2) plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=digits.target) plt.colorbar() # <matplotlib.colorbar.Colorbar at 0x7ff21173ee90>
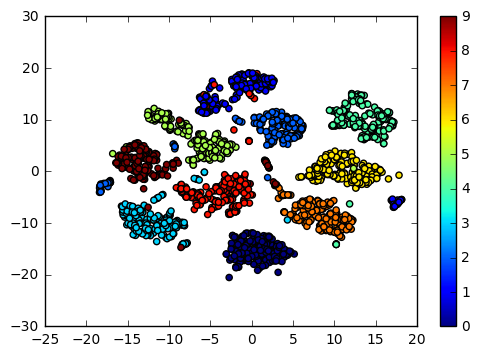
上の結果から、データポイント間の距離をもとに、64次元の特徴量を持つデータを2次元の散布図としてプロットできていることがわかる。