Pari/GPで楕円曲線離散対数を計算してみる
「Pari/GPでECDH鍵交換、ECDSA署名をやってみる」では、数式処理システムPari/GPを使ってECDH鍵交換、ECDSA署名の計算を行った。 これらの楕円曲線暗号は、楕円曲線離散対数問題（ECDLP）と呼ばれる問題が計算量的に困難であることを安全性の根拠としている。 ここでは、実際にbit数の小さな楕円曲線に対して楕円曲線離散対数を計算し、簡単に解けるbit数がどのくらいか調べてみる。
環境
Ubuntu 16.04.1 LTS 64bit版、Pari/GP 2.7.5、Intel Core i5-4200U (1.6GHz * 2 * 2)
$ uname -a Linux vm-ubuntu64 4.4.0-59-generic #80-Ubuntu SMP Fri Jan 6 17:47:47 UTC 2017 x86_64 x86_64 x86_64 GNU/Linux $ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 16.04.1 LTS Release: 16.04 Codename: xenial $ gp --version-short 2.7.5 $ grep "processor\|model name" /proc/cpuinfo processor : 0 model name : Intel(R) Core(TM) i5-4200U CPU @ 1.60GHz processor : 1 model name : Intel(R) Core(TM) i5-4200U CPU @ 1.60GHz processor : 2 model name : Intel(R) Core(TM) i5-4200U CPU @ 1.60GHz processor : 3 model name : Intel(R) Core(TM) i5-4200U CPU @ 1.60GHz
楕円曲線離散対数問題（Elliptic Curve Discrete Logarithm Problem; ECDLP）
楕円曲線離散対数問題とは、有限体（mod p）上で定義した楕円曲線上の点G（生成元）と点Pについて、次の式を満たすnを求めるという問題である。
P = n * G
ここで、記号*は楕円曲線におけるスカラー倍を表す。
通常の（mod p上での）離散対数が乗法群の上で定義されるのに対し、楕円曲線の場合は加法群の上で定義されるため、計算としてはスカラー倍ではあるがアナロジー的に離散対数と呼ばれる。
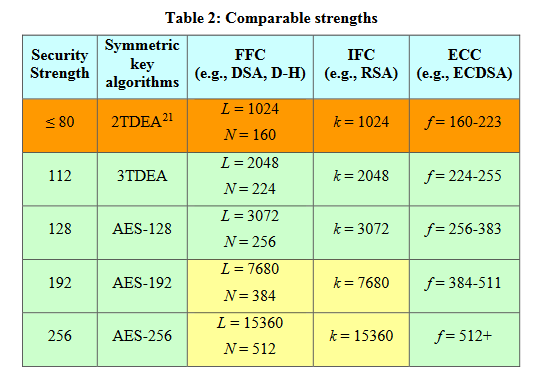
通常の離散対数問題と同様に、楕円曲線離散対数問題を効率的に解く方法は見つかっておらず、十分大きなpをとったときこの計算を現実的な時間で行うことは難しいとされている。 NISTによる等価安全性の評価では、160bitの楕円曲線離散対数問題が1024bitの素因数分解問題に相当するとされており、小さな数でより安全な暗号を構成することができる。
Pari/GPにおける楕円曲線離散対数アルゴリズムの実装
Pari/GPでは、有限体上での楕円曲線に関するさまざまな関数が実装されており、離散対数はelllog関数で求めることができる。
ドキュメントには具体的な計算アルゴリズムが書かれていないため、その詳細をソースコードを追って調べると次のようになる。
6457 GEN
6458 elllog(GEN E, GEN a, GEN g, GEN o)
6459 {
6460 pari_sp av = avma;
6461 GEN fg, r;
6462 checkell_Fq(E); checkellpt(a); checkellpt(g);
6463 fg = ellff_get_field(E);
6464 if (!o) o = ellff_get_o(E);
6465 if (typ(fg)==t_FFELT)
6466 r = FF_elllog(E, a, g, o);
6467 else
6468 {
6469 GEN p = fg, e = ellff_get_a4a6(E);
6470 GEN Pp = FpE_changepointinv(RgE_to_FpE(a,p), gel(e,3), p);
6471 GEN Qp = FpE_changepointinv(RgE_to_FpE(g,p), gel(e,3), p);
6472 r = FpE_log(Pp, Qp, o, gel(e,1), p);
6473 }
6474 return gerepileuptoint(av, r);
6475 }
1426 GEN
1427 FF_elllog(GEN E, GEN P, GEN Q, GEN o)
1428 {
1429 pari_sp av = avma;
1430 GEN fg = ellff_get_field(E), e = ellff_get_a4a6(E);
1431 GEN r,T,p, Pp,Qp, e3;
1432 ulong pp;
1433 _getFF(fg,&T,&p,&pp);
1434 switch(fg[1])
1435 {
1436 case t_FF_FpXQ:
1437 e3 = FqV_to_FpXQV(gel(e,3),T);
1438 Pp = FpXQE_changepointinv(RgE_to_FpXQE(P,T,p), e3, T, p);
1439 Qp = FpXQE_changepointinv(RgE_to_FpXQE(Q,T,p), e3, T, p);
1440 r = FpXQE_log(Pp, Qp, o, gel(e,1), T, p);
1441 break;
1442 case t_FF_F2xq:
1443 Pp = F2xqE_changepointinv(RgE_to_F2xqE(P,T), gel(e,3), T);
1444 Qp = F2xqE_changepointinv(RgE_to_F2xqE(Q,T), gel(e,3), T);
1445 r = F2xqE_log(Pp, Qp, o, gel(e,1), T);
1446 break;
1447 default:
1448 Pp = FlxqE_changepointinv(RgE_to_FlxqE(P,T,pp), gel(e,3), T, pp);
1449 Qp = FlxqE_changepointinv(RgE_to_FlxqE(Q,T,pp), gel(e,3), T, pp);
1450 r = FlxqE_log(Pp, Qp, o, gel(e,1), T, pp);
1451 }
1452 return gerepileupto(av, r);
1453 }
1516 GEN
1517 FpXQE_log(GEN a, GEN b, GEN o, GEN a4, GEN T, GEN p)
1518 {
1519 pari_sp av = avma;
1520 struct _FpXQE e;
1521 e.a4=a4; e.T=T; e.p=p;
1522 return gerepileuptoint(av, gen_PH_log(a, b, o, (void*)&e, &FpXQE_group));
1523 }
577 /* grp->easylog() is an optional trapdoor function that catch easy logarithms*/
578 /* Generic Pohlig-Hellman discrete logarithm*/
579 /* smallest integer n such that g^n=a. Assume g has order ord */
580 GEN
581 gen_PH_log(GEN a, GEN g, GEN ord, void *E, const struct bb_group *grp)
582 {
...
602 for (i=1; i<l; i++)
603 {
...
623 for (j=0;; j++)
624 { /* n_q = sum_{i<j} b_i q^i */
625 b = grp->pow(E,a0, gel(qj,e-j));
626 /* early abort: cheap and very effective */
627 if (j == 0 && !grp->equal1(grp->pow(E,b,q))) {
628 avma = av; return cgetg(1, t_VEC);
629 }
630 b = gen_plog(b, g_q, q, E, grp);
631 if (typ(b) != t_INT) { avma = av; return cgetg(1, t_VEC); }
632 n_q = addii(n_q, mulii(b, gel(qj,j)));
633 if (j == e) break;
634
635 a0 = grp->mul(E,a0, grp->pow(E,ginv0, b));
636 ginv0 = grp->pow(E,ginv0, q);
637 }
638 gel(v,i) = mkintmod(n_q, gel(qj,e+1));
639 }
640 return gerepileuptoint(av, lift(chinese1_coprime_Z(v)));
641 }
520 /*Generic discrete logarithme in a group of prime order p*/
521 GEN
522 gen_plog(GEN x, GEN g, GEN p, void *E, const struct bb_group *grp)
523 {
524 if (grp->easylog)
525 {
526 GEN e = grp->easylog(E, x, g, p);
527 if (e) return e;
528 }
529 if (grp->equal1(x)) return gen_0;
530 if (grp->equal(x,g)) return gen_1;
531 if (expi(p)<32) return gen_Shanks_log(x,g,p,E,grp);
532 return gen_Pollard_log(x, g, p, E, grp);
533 }
要約すると次のようになる。
- Pohlig-Hellmanアルゴリズムで位数の素因数ごとに分解
- それぞれの素因数について、232未満ならBaby-step Giant-stepアルゴリズム、232以上ならPollard’s Rhoアルゴリズムで解く
Pohlig-Hellmanアルゴリズムは、中国の剰余定理を使って計算を高速化するものである。 RSAにおける中国の剰余定理の利用をイメージすると理解しやすい。
Pari/GPで楕円曲線離散対数を計算してみる
ここでは、楕円曲線として次の曲線を考える。
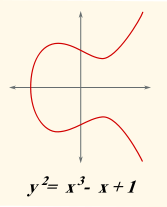(from Wikimedia Commons)
32 bitの素数pをとって計算してみると次のようになる。
$ gp -q ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^32))); ? factor(E.no) [ 2 4] [ 7 1] [ 587 1] [65327 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 0 ms.
ここで、E.noは楕円曲線の位数、E.genはその位数となる生成元を意味する。
上の結果から、正しく楕円曲線離散対数が計算できていることがわかる。
続けて、bit数を徐々に大きくして計算してみる。
? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^64))); ? factor(E.no) [ 2 3] [ 324301 1] [7110193951261 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 40,868 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^72))); ? factor(E.no) [ 2 1] [ 3 3] [ 13 1] [ 37 1] [ 1181 1] [153946902119671 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 2min, 40,652 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^80))); ? factor(E.no) [ 2 2] [ 3 1] [ 11 1] [ 31 1] [ 25111 1] [11765219119332439 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 6min, 3,176 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^88))); ? factor(E.no) [ 3 2] [ 63445780987 1] [541993853311213 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 2min, 10,601 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^96))); ? factor(E.no) [ 2 4] [ 5 2] [ 7 2] [ 79 1] [ 4227397 1] [12103845910958041 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 14min, 24,428 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^104))); ? factor(E.no) [ 2 1] [ 5 1] [ 53 1] [ 83 1] [ 209236176689 1] [2203579946128079 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 5min, 42,409 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^112))); ? factor(E.no) [ 3 2] [ 67 1] [ 214901400149 1] [40068488248358139191 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) ^C *** at top-level: elllog(E,P,G) *** ^------------- *** elllog: user interrupt after 6h, 41min, 47,320 ms *** Break loop: <Return> to continue; 'break' to go back to GP prompt break> ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^120))); ? factor(E.no) [ 3 2] [ 89 1] [ 1847 1] [ 381347 1] [ 31639547057 1] [74464534048783 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 2min, 21,056 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^128))); ? factor(E.no) [ 3 1] [ 41 1] [ 3411655459 1] [ 22003545559 1] [36853310066369891 1] ? G = E.gen[1]; ? P = ellpow(E, G, 17320508); ? elllog(E, P, G) 17320508 ? ## *** last result computed in 28min, 969 ms. ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^136))); ? factor(E.no) [ 3 2] [ 7 1] [ 43 1] [ 5375779 1] [5981760200359529611202066470309 1] ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^144))); ? factor(E.no) [ 2 2] [5575186299632655785385137905034729488784923 1] ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^152))); ? factor(E.no) [ 3 2] [ 99007815273500183 1] [6406891275370833771228590437 1] ? E = ellinit([0,0,0,-1,1] * Mod(1, nextprime(2^160))); ? factor(E.no) [ 3 1] [ 1381217941 1] [352708430713639496569423242667877661011 1] ?
パラメータである素数pを基準に考えると、128bitが約30分で解けていることがわかる。 ただし、Pohlig-Hellmanアルゴリズムの原理からわかるように、実際の計算量に影響するのは位数の素因数のうち最大のものである。 これを考慮すると、56bitが約30分で解けている一方、66bitでは6時間以上の時間がかかることがわかる。
$ python Python 2.7.12 (default, Nov 19 2016, 06:48:10) [GCC 5.4.0 20160609] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>> len(bin(36853310066369891)[2:]) 56 >>> len(bin(40068488248358139191)[2:]) 66
以上からわかるように、安全な楕円曲線パラメータの条件のひとつとして、生成元Gに対する位数の最大素因数が大きい（理想的には位数が素数となる）ことがいえる。 実際に、「Pari/GPでECDH鍵交換、ECDSA署名をやってみる」で用いた楕円曲線パラメータsecp256r1の位数は256 bitの素数となっている。
$ python Python 2.7.12 (default, Nov 19 2016, 06:48:10) [GCC 5.4.0 20160609] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>> n = 0xFFFFFFFF00000000FFFFFFFFFFFFFFFFBCE6FAADA7179E84F3B9CAC2FC632551 >>> n 115792089210356248762697446949407573529996955224135760342422259061068512044369L >>> len(bin(n)[2:]) 256 $ gp -q ? factor(115792089210356248762697446949407573529996955224135760342422259061068512044369) [115792089210356248762697446949407573529996955224135760342422259061068512044369 1]
